
分析 根据等比数列的定义得到an-an-1=2q,为常数,即{an}是等差数列,结合等差数列的性质以及等差数列的前n项和公式进行求解即可.
解答 解:∵数列{2an}是等比数列,∴设公比为q,
则$\frac{{2}^{{a}_{n}}}{{2}^{{a}_{n-1}}}$=2${\;}^{{a}_{n}-{a}_{n-1}}$=q,
则an-an-1=2q,为常数,
则数列{an}是等差数列,
则a4+a2014=2a1009,
由a4+a1009+a2014=$\frac{3}{2}$,得3a1009=$\frac{3}{2}$,
即a1009=$\frac{1}{2}$,
则S2017=$\frac{2017({a}_{1}+{a}_{2017})}{2}$=$\frac{2017×2{a}_{1009}}{2}$=$\frac{2017}{2}$,
故答案为:$\frac{2017}{2}$
点评 本题主要考查数列求和的计算,根据等比数列和等差数列的定义判断数列{an}是等差数列,以及利用等差数列的性质是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)-f(1)<0 | B. | f(-1)-f(1)>0 | C. | f(-1)+f(1)<0 | D. | f(-1)+f(1)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
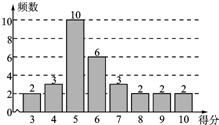 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为| A. | me=mo | B. | mo<me | C. | me<mo | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
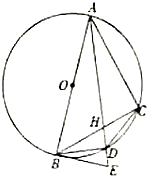 如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD、CD.
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD、CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com