
分析 (Ⅰ)将函数f(x)的图象向左平移$\frac{1}{3}$个单位,得到函数g(x)=f(x+$\frac{1}{3}$)=x3-$\frac{4}{3}$x的图象,根据g(x)的奇偶性判证出结论即可;
(Ⅱ)求出f(x)的导数,通过讨论a的范围求出函数的单调区间即可.
解答 (Ⅰ)证明:当a=3时,f(x)=x3-x2-x+$\frac{11}{27}$,
将函数f(x)的图象向左平移$\frac{1}{3}$个单位,
得到函数g(x)=f(x+$\frac{1}{3}$)=x3-$\frac{4}{3}$x的图象,
∵任意x∈R,-x∈R且g(-x)=-g(x),
∴g(x)是奇函数,图象关于原点对称,
∴函数f(x)的图象关于($\frac{1}{3}$,0)对称;
(Ⅱ)解:由f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$(a-1)x2-x+$\frac{11}{27}$,
得:f′(x)=ax2-(a-1)x-1=(x-1)(ax+1),
①a=-1时,f′(x)=-(x-1)2≤0,
∴f(x)在R递减;
②当a<-1时,令f′(x)>0,解得:-$\frac{1}{a}$<x<1,
令f′(x)<0,解得:x>1或x<-$\frac{1}{a}$,
∴f(x)在(-∞,-$\frac{1}{a}$)递减,在(-$\frac{1}{a}$,1)递增,在(1,+∞)递减;
③当-1<a<0时,令f′(x)>0,解得:1<x<-$\frac{1}{a}$,
令f′(x)<0,解得:x<1或x>-$\frac{1}{a}$,
∴f(x)在(-∞,1)递减,在(1,-$\frac{1}{a}$)递增,在(-$\frac{1}{a}$,+∞)递减.
点评 本题考查了函数的奇偶性,考查函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{BA}$=$\overrightarrow 0$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
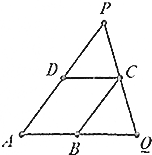 某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.
某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
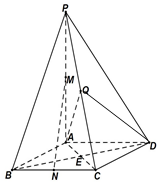 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com