
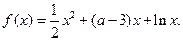
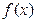 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数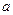 的最小值;
的最小值;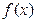 的图象上是否存在不同两点
的图象上是否存在不同两点 ,线段
,线段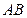 的中点的横坐标为
的中点的横坐标为 ,直线
,直线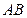 的斜率为
的斜率为 ,有
,有 成立?若存在,请求出
成立?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
A.(-2,2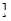 | B.(-∞,2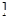 | C.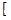 -2,2 -2,2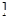 | D.(-∞,-2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.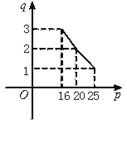
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com