练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数（，是自然对数的底数，）存在唯一的零点，则实数的取值范围为______．

    【答案】

    【解析】

    函数存在唯一的零点等价于函数与函数的图像只有一个交点．∵，，∴函数与函数的图像的唯一交点为．对求导，可得的单调性及斜率范围，又是最小正周期为2．最大值为的正弦型函数，画出草图，比较与在x=1处斜率即可.

    函数（，是自然对数的底数，）存在唯一的零点等价于函数与函数的图像只有一个交点．

    ∵，，

    ∴函数与函数的图像的唯一交点为．

    又∵，且，，

    ∴在上恒小于零，即在上为单调递减函数．

    又∵，当且仅当，即时等号成立，且是最小正周期为2．最大值为的正弦型函数，

    ∴可得函数与函数的大致图像如图所示．

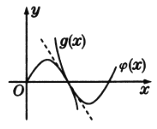
    ∴要使函数与函数的图像只有唯一一个交点，则．

    ∵，，

    ∴，解得．

    对∵，∴实数的取值范围为．

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，椭圆的右焦点、右顶点分别为F，A，过原点的直线与椭圆C交于点P、Q（点P在第一象限内），连结PA，QF．若，的面积是面积的3倍．

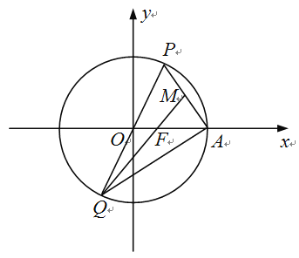
    （1）求椭圆C的标准方程；

    （2）已知M为线段PA的中点，连结QA，QM．

    ①求证：Q，F，M三点共线；

    ②记直线QP，QM，QA的斜率分别为，，，若，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形中，，，，，，点是线段的中点，将，分别沿，

    向上折起，使，重合于点，得到三棱锥．试在三棱锥中，

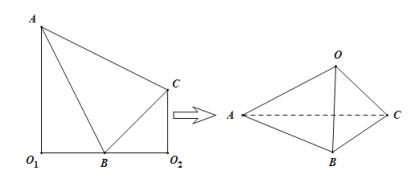
    （1）证明：平面平面；

    （2）求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列是首项为1的等差数列，数列是公比不为1的等比数列，且满足，，

    （1）求数列，的通项公式；

    （2）令，记数列的前n项和为，求证：对任意的，都有；

    （3）若数列满足，，记，是否存在整数，使得对任意的 都有成立？若存在，求出的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如下表：

    （年龄/岁）

    26

    27

    39

    41

    49

    53

    56

    58

    60

    61

    （脂肪含量/%）

    14.5

    17.8

    21.2

    25.9

    26.3

    29.6

    31.4

    33.5

    35.2

    34.6

    根据上表的数据得到如下的散点图.

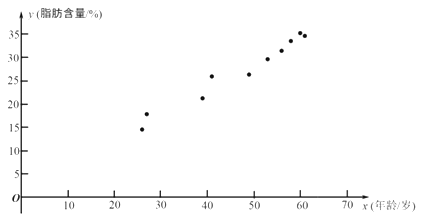
    （1）根据上表中的样本数据及其散点图：

    （i）求；

    （i）计算样本相关系数（精确到0.01），并刻画它们的相关程度.

    （2）若关于的线性回归方程为，求的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量.

    附：参考数据：，，，，，，

    参考公式：相关系数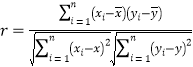

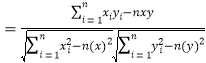
    回归方程中斜率和截距的最小二乘估计公式分别为，.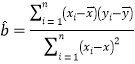

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，倾斜角为的直线经过坐标原点，曲线的参数方程为（为参数）.以点为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求与的极坐标方程；

    （2）设与的交点为、，与的交点为、，且，求值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为加快新能源汽车产业发展，推进节能减排，某年国家对消费者购买新能源汽车给予补贴，其中对纯电动乘用车补贴标准如下表：

    新能源汽车补贴标准

    车辆类型

    续驶里程

    纯电动乘用车

    3.5万元/辆

    5万元/辆

    6万元/辆

    某校研究学习小组从汽车市场上随机选取了辆纯电动乘用车，根据其续驶里程（单次充电后能行驶的最大里程）作出了如下的频率与频数的统计表：

    分组

    频数

    频率

    2

    0.2

    5

    合计

    1

    （1）若从这辆纯电动乘用车中任选2辆，求选到的2辆车续驶里程都不低于150km的概率．

    （2）若以频率作为概率，设为购买一辆纯电动乘用车获得的补贴，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（ ）

    A.20°B.40°

    C.50°D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后，发现一天中环境综合污染指数与时刻（时）的关系为，，其中是与气象有关的参数，且．若用每天的最大值为当天的综合污染指数，并记作．

    （1）令，，求的取值范围；

    （2）求的表达式，并规定当时为综合污染指数不超标，求当在什么范围内时，该市市中心的综合污染指数不超标．

    查看答案和解析>>

    同步练习册答案