【题目】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（ ）
A.20°B.40°
C.50°D.90°
教材全解字词句篇系列答案科目：高中数学 来源： 题型：
【题目】某地区对当地的某种土特产的销售量y（吨）和销售单价x（元/千克）之间的关系进行了调查，得到下表中的数据：
销售单价x（元/千克） | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y（吨） | 5 | 6 | 8 | 10 | 11 | 14.1 |
（1）根据前5组数据，求出y关于x的回归直线方程．
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5，则认为回归直线方程是理想的，试问（1）中得到的回归直线方程是否理想？
（3）如果销售量y（吨）和销售单价x（元/千克）之间仍然服从（1）中的关系，进货成本为2.5元/千克，且货源充足（未售完的部分可按成本价全部售出），为了使利润最大，请你就如何确定销售单价给出合理建议．（每千克销售单价不超过12元）
参考公式：回归直线方程
，其中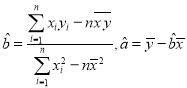
．
参考数据：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】祖暅是我国南北朝时期杰出的数学家和天文学家祖冲之的儿子，他提出了一条原理：“幂势既同幂，则积不容异”.这里的“幂”指水平截面的面积，“势”指高.这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体体积相等.一般大型热电厂的冷却塔大都采用双曲线型.设某双曲线型冷却塔是曲线
与直线
， 
和
所围成的平面图形绕
轴旋转一周所得，如图所示.试应用祖暅原理类比求球体体积公式的方法，求出此冷却塔的体积为_______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)＝Asin(ωx＋φ)(A≠0，ω＞0，
＜φ＜
)的图象关于直线
对称，它的最小正周期为π，则( )
A. f(x)的图象过点(0，
) B. f(x)在
上是减函数
C. f(x)的一个对称中心是
D. f(x)的一个对称中心是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥PABCD的底面为正方形，PD底面ABCD．设平面PAD与平面PBC的交线为
．
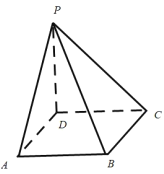
（1）证明：平面PDC；
（2）已知PDAD1，Q为上的点，QB=
，求PB与平面QCD所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
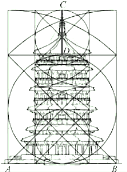
【题目】在《周髀算经》中，把圆及其内接正方形称为圆方图，把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑，它的正面图如下图所示.以该木塔底层的边
作正方形，以点
或点
为圆心，以这个正方形的对角线为半径作圆，会发现塔的高度正好跟此对角线长度相等.以该木塔底层的边作正方形，会发现该正方形与其内切圆的一个切点
正好位于塔身和塔顶的分界线上.经测量发现，木塔底层的边不少于47.5米，塔顶
到点的距离不超过19.9米，则该木塔的高度可能是（参考数据：
）（ ）
A.66.1米B.67.3米C.68.5米D.69.0米
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，过点P（1，2）的直线l的参数方程为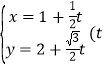
为参数）．以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为
．
（1）求直线l的普通方程和曲线C的直角坐标方程；
（2）若直线l与曲线C相交于M，N两点，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
