
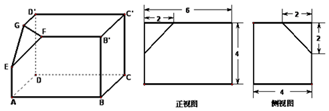
分析 (1)根据几何体的结构特征与它的正(主)视图和侧(左)视图可得其侧视图.
(2)由题意可得:所求多面体体积V=V长方体-V正三棱锥,该多面体的体积和表面积为长方体的表面积为减去截去的表面积
解答 解:(1)该多面体的俯视图如下;
(2):所求多面体体积V=V长方体-V正三棱锥=4×4×4-$\frac{1}{3}$×($\frac{1}{2}$×2×2)×2=$\frac{284}{3}c{m}^{3}$
长方体的表面积为128,截去的表面积为6,等边三角形面积为$2\sqrt{3}$
几何体的表面积为122+$2\sqrt{3}$.
点评 本题考查该多面体的三视图,多面体的体积、表面积的计算,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 22017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
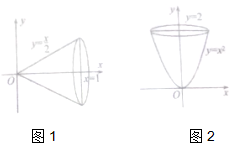 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com