
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( )
A. | B. | C. | D.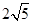 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
如图,在三棱锥S﹣ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知 ,
, ,
, 为三条不同的直线,
为三条不同的直线, ,
,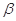 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( )
A. ⊥ ⊥ , , ⊥ ⊥ ,且 ,且 ,则 ,则 ⊥ ⊥ . . |
B.若平面 内有不共线的三点到平面 内有不共线的三点到平面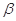 的距离相等,则 的距离相等,则 . . |
C.若 , , ,则 ,则 . . |
D.若 , , ,则 ,则 . . |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,在棱长为 的正方体
的正方体 中,
中, 为
为 的中点,
的中点,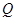 为
为 上任意一点,
上任意一点, 为
为 上两点,且
上两点,且 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )
A.点 到平面 到平面 的距离 的距离 |
B.直线 与平面 与平面 所成的角 所成的角 |
C.三棱锥 的体积 的体积 |
D. 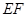 的面积 的面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设a,b为两条不重合的直线,α,β为两个不重合的平面,下列命题中为真命题的是( )
| A.若a,b与α所成的角相等,则a∥b |
| B.若a∥α,b∥β,α∥β,则a∥b |
| C.若a?α,b?β,a∥b,则α∥β |
| D.若a⊥α,b⊥β,α⊥β,则a⊥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
右图为一简单组合体,其底面ABCD为正方形, 平面
平面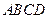 ,
,  ,且
,且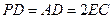 ="2" .
="2" .
(1)答题卡指定的方框内画出该几何体的三视图;
(2)求四棱锥B-CEPD的体积. 

查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知m,n为两条不同的直线, 为两个不同的平面,
为两个不同的平面, ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
A.若m//n,则 |
B.若 ,则 ,则 |
C.若 相交,则 相交,则 相交 相交 |
D.若 相交,则 相交,则 相交 相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知α,β是两个不同的平面,给出下列四个条件:
①存在一条直线a,a⊥α,a⊥β;
②存在一个平面γ,γ⊥α,γ⊥β;
③存在两条平行直线a,b,a?α,b?β,a∥β,b∥α;
④存在两条异面直线a,b,a?α,b?β,a∥β,b∥α.
可以推出α∥β的是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com