练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知满足，则的形状是（     ）

    A．等腰三角形     B．直角三角形   C．等边三角形  D．等腰三角形或直角三角形


    A；   

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数，．

    (1)若函数在上单调递增，求实数的取值范围；

    (2) 若直线是函数图象的切线，求的最小值；

    (3)当时，若与的图象有两个交点，求证：．

    （取为，取为，取为）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知抛物线y2＝－x与直线y＝k(x＋1)相交于A、B两点．

    (1)求证：OA⊥OB；

    (2)当△OAB的面积等于时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　．

    已知,且,则　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数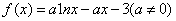

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）若函数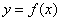的图像在点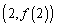处的切线的倾斜角为45°，那么实数m在什么范围取值时，函数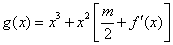在区间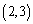内总存在极值？

    （Ⅲ）求证：．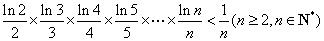

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人为了观看2010年南非足球世界杯,从2006年起,每年的5月1日到银行存入a元的定期储蓄,若年利率为p且保持不变,并约定每年到期,存款的本息均自动转为新的一年的定期,到2010年的5月1日将所有存款及利息全部取出,则可取出钱(元)的总数为(     )

    A. a(1+p)4                         B.a(1+p)5   

      C.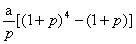             D.

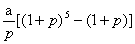
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC的内角A、B、C所对的边分别为a，b，c，且a=2， cosB=．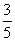

    (1)若b=4，求sinA的值；

     (2) 若△ABC的面积S△ABC=4，求b，c的值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若不等式对任意正整数n恒成立。则实数a的取值范围是(   )

      A .           B .          C.  [         D .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题：“三角形三个内角中至少有一个不大于60°”时，应假设(　　)

    A．三个内角都不大于60°　　　　B．三个内角都大于60°

    C．三个内角至多有一个大于60°　D．三个内角至多有两个大于60°

    查看答案和解析>>

    同步练习册答案