
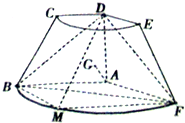
 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧 |
| BF |
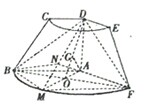 (Ⅰ)证明:连接AM交BF于点O,则
(Ⅰ)证明:连接AM交BF于点O,则 |
| BF |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |


科目:高中数学 来源: 题型:
 某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )| A、11小时 | B、13小时 |
| C、15小时 | D、10小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| π |
| 6 |
| π |
| 4 |
| b |
| π |
| 6 |
| π |
| 4 |
| a |
| b |
| π |
| 12 |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OC |
| OA |
| OB |
| OD |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| b3 |
| 1 |
| b4 |
| 1 |
| b5 |
| 1 |
| bn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com