练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．函数y=x2+bx-4在（-∞，-1]上是减函数，在[-1，+∞）上是增函数，则（　　）
    A．b＜0B．b＞0C．b=0D．b的符号不定

    分析 由题意得出对称轴为x=-1，从而解出b=2．

    解答 解：由题意得；
    对称轴x=-$\frac{b}{2}$=-1，
    解得：b=2＞0，
    故选B．

    点评 本题考察了二次函数的性质问题，可结合图象一目了然，本题是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

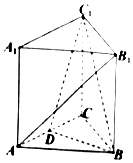    6．如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，△ABC为正三角形，AA1=AB=6，点D为AC的中点．
    （1）求证：平面BC1D⊥平面ACC1A1；
    （2）求三棱锥C-BC1D的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在△ABC中，角A，B，C的对边分别为a，b，c，∠B=$\frac{π}{3}$，c=4，$\overrightarrow{CB}$$•\overrightarrow{CA}$=-1，则b=$\sqrt{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．如图，一个正五角星薄片（其对称轴与水面垂直）匀速地升出水面，记t时时刻五角星露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S′（t）的图象大致为（　　）
    A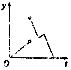．B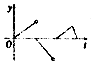．C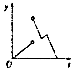．D．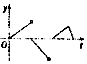

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的左焦点为F，点P为双曲线右支上一点，点A满足$\overrightarrow{AP}$•$\overrightarrow{AF}$=0，则点A到原点的最近距离为（　　）
    A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知y=f（x）在定义域（-1，1）上是减函数，且f（1-a）＜f（2a-1），则a的取值范围是（　　）
    A．$a＜\frac{2}{3}$B．a＞0C．$0＜a＜\frac{2}{3}$D．a＜0或$a＞\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．如图所示，在边长为1的正方形f（x）中任取一点f（x），则点[-1，1）恰好取自阴影部分的概率为$\frac{1}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

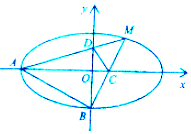    5．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，过椭圆的焦点且与长轴垂直的弦长为1．
    （1）求椭圆C的方程；
    （2）设点M为椭圆上位于第一象限内一动点，A，B分别为椭圆的左顶点和下顶点，直线MB与x轴交于点C，直线MA与轴交于点D，求证：四边形ABCD的面积为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．以直角坐标系xOy的原点为极点，x轴的正半轴为极轴建立极坐标系，两坐标系中的单位长度相同．已知点A的极坐标为（${\sqrt{2}$，$\frac{π}{4}}$），曲线C在直角坐标系下参数方程为$\left\{\begin{array}{l}x=\sqrt{2}cost\\ y=\sqrt{2}sint\end{array}$（t为参数），曲线C在点A处的切线为l．
    （1）求切线l的极坐标方程；
    （2）已知点P直角坐标为（-$\frac{1}{4}$，$\frac{{\sqrt{3}}}{4}$），过点P任作一直线交曲线C于A，B两点，求|AB|的最小值．

    查看答案和解析>>

    同步练习册答案