
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 设F'为双曲线的右焦点,M为PF的中点,则|PF|-|PF'|=2$\sqrt{2}$,|OM|=$\frac{1}{2}$|PF'|,点A在以PF为直径的圆上,故当O,A,M共线时,可得OA取得最小值MA-OM.
解答 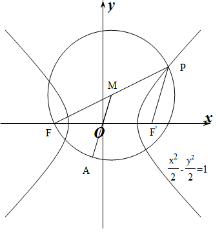 解:双曲线的左焦点为F(-2,0),右焦点为F′(2,0),
解:双曲线的左焦点为F(-2,0),右焦点为F′(2,0),
连接PF′,PF,设PF的中点为M,
∵$\overrightarrow{AP}$•$\overrightarrow{AF}$=0,
∴点A在以PF为直径的圆M上,
∴当AOM三点共线时,OA取得最小值,最小值为MA-OM.
设圆M的半径为r,则PF=2r,MA=r.
∵P在双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1上,
∴PF-PF′=2$\sqrt{2}$,
∴PF′=2r-2$\sqrt{2}$,
∵OM是△PFF′的中位线,
∴OM=$\frac{1}{2}$PF′=r-$\sqrt{2}$,
∴MA-OM=r-(r-$\sqrt{2}$)=$\sqrt{2}$.
故选:B.
点评 本题考查两点的距离的最小值的求法,注意运用双曲线的定义和圆的性质,及三点共线取得最小值,考查运算能力,属于中档题


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
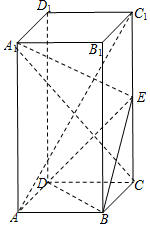 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com