练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的外接球的表面积为1025π．

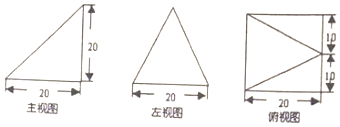
    分析 几何体为四棱锥，根据三视图判断四棱锥的结构特征，依据结构特征判定外接球的球心位置，求出外接球的半径，代入球的表面积公式计算．

    解答 解：由三视图知：几何体为四棱锥，且四棱锥的一个侧面与底面垂直，高为8，如图：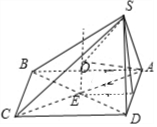

    设O为外接球的球心，OE=x，
    则OA=$\sqrt{{x}^{2}+200}$=OS=$\sqrt{100+{（20-x）}^{2}}$⇒x=7.5，
    ∴其外接球的半径R=$\frac{5\sqrt{41}}{2}$．
    ∴外接球的表面积S=4πR2=1025π．
    故答案为：1025π

    点评 本题考查了由三视图求几何体外接球的表面积，根据三视图判断几何体的结构特征并求得外接球的半径是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．设函数f（x）的定义域为R，且|f（x）|是偶函数，则下列结论中正确的是（　　）
    A．f（x）是偶函数B．f（x）是奇函数
    C．|f（x-1）|的图象关于直线x=1对称D．|f（x）+1|的图象关于点（0，1）对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的左焦点为F，点P为双曲线右支上一点，点A满足$\overrightarrow{AP}$•$\overrightarrow{AF}$=0，则点A到原点的最近距离为（　　）
    A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．如图所示，在边长为1的正方形f（x）中任取一点f（x），则点[-1，1）恰好取自阴影部分的概率为$\frac{1}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}，x≥0}\\{{2}^{x}，x＜0}\end{array}\right.$，则f（f（-log23））=（　　）
    A．$\frac{3-\sqrt{3}}{3}$B．$\frac{3}{2}$C．1-$\sqrt{3}$D．$\sqrt{3}$-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

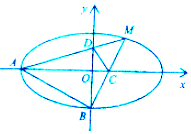    5．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，过椭圆的焦点且与长轴垂直的弦长为1．
    （1）求椭圆C的方程；
    （2）设点M为椭圆上位于第一象限内一动点，A，B分别为椭圆的左顶点和下顶点，直线MB与x轴交于点C，直线MA与轴交于点D，求证：四边形ABCD的面积为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知等差数列{an}的公差d=2，a3=5，数列{bn}，bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$，则数列{bn}的前10项的和为（　　）
    A．$\frac{10}{21}$B．$\frac{20}{21}$C．$\frac{10}{19}$D．$\frac{20}{19}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在直角坐标系中，椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点分别为F1，F2，其中F2也是抛物线C2：y2=4x的焦点，点P为C1与C2在第一象限的交点，且$|P{F_2}|=\frac{5}{3}$．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）过F2且与坐标轴不垂直的直线交椭圆于M、N两点，若线段OF2上存在定点T（t，0）使得以TM、TN为邻边的四边形是菱形，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．在空间中，下列命题错误的是（　　）
    A．过直线外一点有且只有一条直线与已知直线平行
    B．不公线的三个点确定一个平面
    C．如果两条直线垂直于同一条直线，那么这两条直线平行
    D．如果两个平面垂直于同一个平面，那么这两个平面可能互相垂直

    查看答案和解析>>

    同步练习册答案