
已知函数f(x)=x3﹣3x.
(1)求函数f(x)在[﹣3,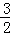 ]上的最大值和最小值;
]上的最大值和最小值;
(2)过点P(2,﹣6)作曲线y=f(x)的切线,求此切线的方程.
(1)f(x)min=﹣18,f(x)max=2.
(2)y=3x或y=24x﹣54.
【解析】
试题分析:(1)先求出函数的导数,然后判断在要求区间内导数的正负情况,从而可得出最大值与最小值.
(2)根据导函数的定义可求出切线的斜率,然后根据点P的坐标可求出切线的方程.
【解析】
(1)f′(x)=3(x+1)(x﹣1),
当x∈[﹣3,﹣1)或x∈(1,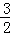 ]时,f′(x)>0,
]时,f′(x)>0,
∴[﹣3,﹣1],[1,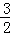 ]为函数f(x)的单调增区间,
]为函数f(x)的单调增区间,
当x∈(﹣1,1)为函数f(x)的单调减区间,
又∵f(﹣3)=﹣18,f(﹣1)=2,f(1)=﹣2,f(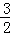 )=﹣
)=﹣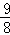 ,
,
所以当x=﹣3时,f(x)min=﹣18,
当x=﹣1时,f(x)max=2.
(2)由于点P不在曲线上,故设切点为(x0,y0)则切线方程为:y﹣y0=3(x02﹣1)(x﹣x0)①,
又点P(2,﹣6)在此切线上,以及y0=x03﹣3x0代入①,解得:x0=0或3,
故此直线的斜率为3或24,
故可求得切线的方程为y=3x或y=24x﹣54.


科目:高中数学 来源:[同步]2014年苏教版必修三 2.3 总体特征数的估计练习卷(解析版) 题型:填空题
甲.乙两名射手在相同条件下射击10次,环数如下:
甲:7 8 8 9 9 9 9 10 10 10
乙:7 7 8 9 9 9 10 10 10 10
问哪一名选手的成绩稳定? .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷(解析版) 题型:解答题
设全集U={2,4,3﹣x},M={2,x2﹣x+2},∁UM={1},求x.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
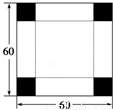
如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
把总长为16m的篱笆,要围成一个矩形场地,则矩形场地的最大面积是 m2.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.2导数的运算练习卷(解析版) 题型:解答题
已知函数f1(x)=sinx,且fn+1(x)=fn′(x),其中n∈N*,求f1(x)+f2(x)+…+f100(x)的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:选择题
(2009•四川)已知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2 B.3 C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com