
分析 (Ⅰ)由题意得,焦点为椭圆的左焦点,即F(-c,0),设弦与椭圆的交点为A(x1,y1),B(x2,y2),分别代入椭圆方程相减可得:$-\frac{b^2}{a^2}=\frac{{{y_1}^2-{y_2}^2}}{{{x_1}^2-{x_2}^2}}$.由点M平分弦AB,弦经过焦点,利用中点坐标公式、斜率计算公式可得:$\frac{b^2}{a^2}=\frac{1}{{6({c-\frac{2}{3}})}}$,又$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,a2-b2=c2,解出即可得出.
(Ⅱ)设点N坐标为(x1,y1),由对称性,不妨设y1>0,由$\frac{x^2}{2}+{y^2}=1$得椭圆上半部分的方程为$y=\sqrt{1-\frac{x^2}{2}}$,利用导数的几何意义与斜率计算公式可得:N点处的切线方程为$y-{y_1}=\frac{{-{x_1}}}{{2{y_1}}}({x-{x_1}})$,过F且垂直于FN的直线方程为$y=-\frac{{{x_1}+1}}{y_1}({x+1})$,结合$\frac{{{x_1}^2}}{2}+{y_1}^2=1$,即可得出.
解答 (Ⅰ)解:由题意得,焦点为椭圆的左焦点,即F(-c,0),
设弦与椭圆的交点为A(x1,y1),B(x2,y2),
代入椭圆方程得$\frac{{{x_1}^2}}{a^2}+\frac{{{y_1}^2}}{b^2}=1$…①$\frac{{{x_2}^2}}{a^2}+\frac{{{y_2}^2}}{b^2}=1$…②
①式-②式,得$-\frac{b^2}{a^2}=\frac{{{y_1}^2-{y_2}^2}}{{{x_1}^2-{x_2}^2}}$…③
∵点M平分弦AB,弦经过焦点,
∴$\frac{{{x_1}+{x_2}}}{2}=-\frac{2}{3}$,$\frac{{{y_1}+{y_2}}}{2}=\frac{1}{3}$,$\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{\frac{1}{3}}}{{-\frac{2}{3}+c}}$,
代入③式得,$-\frac{b^2}{a^2}=\frac{{\frac{2}{3}×\frac{1}{3}}}{{-\frac{4}{3}×({-\frac{2}{3}+c})}}$,即$\frac{b^2}{a^2}=\frac{1}{{6({c-\frac{2}{3}})}}$,
又∵$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,a2-b2=c2,∴${c^2}={b^2}=\frac{1}{2}{a^2}$,∴$\frac{1}{2}=\frac{1}{{6({c-\frac{2}{3}})}}$,
即c=1,$a=\sqrt{2}$,∴椭圆方程为$\frac{x^2}{2}+{y^2}=1$.
(Ⅱ)证明:设点A坐标为(x1,y1),由对称性,不妨设y1>0,
由$\frac{x^2}{2}+{y^2}=1$得椭圆上半部分的方程为$y=\sqrt{1-\frac{x^2}{2}}$,$y'=\frac{1}{2}•\frac{1}{{\sqrt{1-\frac{x^2}{2}}}}•({-x})=\frac{-x}{{2\sqrt{1-\frac{x^2}{2}}}}$,
∴${k_切}=\frac{{-{x_1}}}{{2\sqrt{1-\frac{{{x_1}^2}}{2}}}}=\frac{{-{x_1}}}{{2{y_1}}}$,
∴A点处的切线方程为$y-{y_1}=\frac{{-{x_1}}}{{2{y_1}}}({x-{x_1}})$…①
过F且垂直于FA的直线方程为$y=-\frac{{{x_1}+1}}{y_1}({x+1})$…②
由①②两式,消去y得${y_1}=-\frac{{{x_1}+1}}{y_1}({x+1})+\frac{x_1}{{2{y_1}}}•({x-{x_1}})$…③
其中$\frac{{{x_1}^2}}{2}+{y_1}^2=1$,代入③式,可得x=-2
∴点P在定直线x=-2上
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交相切问题、“差点法”、导数的几何意义、中点坐标公式、斜率计算公式,考查了推理能力与计算能力,属于难题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{π}$,2] | B. | (-∞,$\frac{2}{π}$)∪[2,+∞) | C. | [0,$\frac{2}{π}$) | D. | (-∞,0)∪[$\frac{2}{π}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 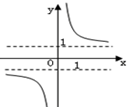 | B. | 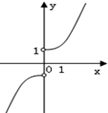 | C. | 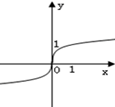 | D. | 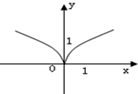 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com