
| A. | 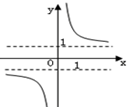 | B. | 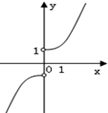 | C. | 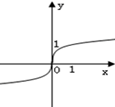 | D. | 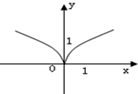 |
分析 令 t=f(x)-ex,由 f[f(x)-ex]=f(t)=1,求得t=0,可得f(x)的解析式,从而求得g(x)的解析式,再根据函数的定义域、单调性、值域,判断函数g(x)的图象特征.
解答 解:令 t=f(x)-ex,则f(x)=t+ex,由题意可得 f[f(x)-ex]=f(t)=1,
∴t+et=1,即 et=1-t,
∴t=0,即f(x)=ex.
∴函数g(x)=$\frac{f(x)+f(-x)}{f(x)-f(-x)}$=$\frac{{e}^{x}{+e}^{-x}}{{e}^{x}{-e}^{-x}}$=$\frac{{e}^{2x}+1}{{e}^{2x}-1}$=1+$\frac{2}{{e}^{2x}-1}$ (x≠0)),故排除C、D.
∴g(-x)=-g(x),故g(x)为奇函数,故它的图象关于原点对称.
当x>0时,g(x)为单调递减函数,故排除B.
∵$\frac{2}{{e}^{2x}-1}$>0,∴g(x)>1,
故选:A.
点评 本题主要考查求函数的解析式,根据函数的定义域、单调性、值域,判断函数的图象特征,属于中档题.


科目:高中数学 来源: 题型:填空题
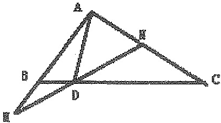 如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.
如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{21}$ | B. | $\frac{2\sqrt{29}}{3}$ | C. | 2$\sqrt{21}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com