
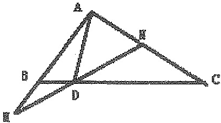
 如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.
如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3. 分析 先确定λ,μ的关系,再利用导数法,即可求出λ+3μ的最小值.
解答 解:∵若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),∴$\overrightarrow{MB}$=$\overrightarrow{MD}$+$\overrightarrow{DB}$=(1-λ)$\overrightarrow{AB}$,M,D,N三点共线,
∴存在实数k,使$\overrightarrow{MD}$=k$\overrightarrow{MN}$=k($\overrightarrow{AN}$-$\overrightarrow{AM}$)=-kλ$\overrightarrow{AB}$+kμ$\overrightarrow{AC}$.
∵$\overrightarrow{DB}$=$\frac{1}{4}$$\overrightarrow{CB}$=$\frac{1}{4}$$\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AC}$,∴($\frac{1}{4}$-kλ)$\overrightarrow{AB}$+(kμ-$\frac{1}{4}$)$\overrightarrow{AC}$=(1-λ)$\overrightarrow{AB}$,
∴$\frac{1}{4}$-kλ=1-λ,kμ-$\frac{1}{4}$=0,
∴μ=$\frac{λ}{4λ-3}$,λ+3μ=λ+$\frac{3λ}{4λ-3}$.
设f(λ)=λ+$\frac{3λ}{4λ-3}$,λ>0,则f′(λ)=1+$\frac{-9}{{(4λ-3)}^{2}}$,
令f′(λ)=0得,λ=0,或 λ=$\frac{3}{2}$.
在(0,$\frac{3}{2}$)上,f′(λ)<0; 在( $\frac{3}{2}$,+∞)时,f′(λ)>0;
∴λ=$\frac{3}{2}$时,f(λ)取极小值,也是最小值;
∴f(λ)的最小值为 3,即λ+3μ的最小值是3,
故答案为:3.
点评 考查向量的加法、减法运算,共线向量基本定理,以及平面向量基本定理,通过求导求函数的最小值的方法及过程,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆过点$({2\sqrt{3},1})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{9}$ | C. | -9 | D. | -$\frac{1}{9}$或-9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{13}{9}$ | C. | 1 | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{π}$,2] | B. | (-∞,$\frac{2}{π}$)∪[2,+∞) | C. | [0,$\frac{2}{π}$) | D. | (-∞,0)∪[$\frac{2}{π}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 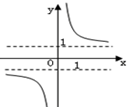 | B. | 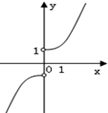 | C. | 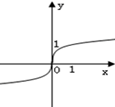 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com