
分析 (1)构造函数,求导数,利用函数的单调性,即可证明结论;
(2)不妨设x1<x2,$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′($\frac{{x}_{1}+{x}_{2}}{2}$)?$\frac{{x}_{2}ln{x}_{2}-{x}_{1}ln{x}_{1}}{{x}_{2}-{x}_{1}}$<ln$\frac{{x}_{1}+{x}_{2}}{2}$+1,即x2lnx2-x1lnx1<x2ln$\frac{{x}_{1}+{x}_{2}}{2}$-x1ln$\frac{{x}_{1}+{x}_{2}}{2}$+x2-x1,两边同除以x1得$\frac{{x}_{2}}{{x}_{1}}$ln$\frac{2•\frac{{x}_{2}}{{x}_{1}}}{1+\frac{{x}_{2}}{{x}_{1}}}$<ln$\frac{2}{1+\frac{{x}_{2}}{{x}_{1}}}$+$\frac{{x}_{2}}{{x}_{1}}$-1,令$\frac{{x}_{2}}{{x}_{1}}$=t,则t>1,即证:tln$\frac{2t}{1+t}$<ln$\frac{2}{1+t}$+t-1,令g(t)=$\frac{2t}{1+t}$-ln$\frac{2}{1+t}$-t+1,利用导数证明g(t)<0即可.
解答 证明:(1)(1)当x∈[-1,0]时,求证:$\frac{1+x}{1-x}$≤e2x≤$\frac{1}{(1-x)^{2}}$;
构造函数g(x)=$\frac{1+x}{1-x}$-e2x,则g′(x)=$\frac{2}{(1-x)^{2}}$-2e2x,∵x∈[-1,0],∴g′(x)≥0,
∴g(x)在区间[-1,0]上单调递增,∴g(x)≤g(0)=0,∴$\frac{1+x}{1-x}$≤e2x;
构造函数h(x)=e2x-$\frac{1}{(1-x)^{2}}$,则h′(x)=2e2x+$\frac{2}{(1-x)^{3}}$>0,
∴h(x)在区间[-1,0]上单调递增,∴h(x)≤h(0)=0,∴e2x≤$\frac{1}{(1-x)^{2}}$;
∴$\frac{1+x}{1-x}$≤e2x≤$\frac{1}{(1-x)^{2}}$;
(2)不妨设x1<x2,
$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′($\frac{{x}_{1}+{x}_{2}}{2}$)?$\frac{{x}_{2}ln{x}_{2}-{x}_{1}ln{x}_{1}}{{x}_{2}-{x}_{1}}$<ln$\frac{{x}_{1}+{x}_{2}}{2}$+1,
即x2lnx2-x1lnx1<x2ln$\frac{{x}_{1}+{x}_{2}}{2}$-x1ln$\frac{{x}_{1}+{x}_{2}}{2}$+x2-x1,
∴x2ln$\frac{2{x}_{2}}{{x}_{1}+{x}_{2}}$<x1ln$\frac{2{x}_{1}}{{x}_{1}+{x}_{2}}$+x2-x1,
两边同除以x1得$\frac{{x}_{2}}{{x}_{1}}$ln$\frac{2•\frac{{x}_{2}}{{x}_{1}}}{1+\frac{{x}_{2}}{{x}_{1}}}$<ln$\frac{2}{1+\frac{{x}_{2}}{{x}_{1}}}$+$\frac{{x}_{2}}{{x}_{1}}$-1,
令$\frac{{x}_{2}}{{x}_{1}}$=t,则t>1,即证:tln$\frac{2t}{1+t}$<ln$\frac{2}{1+t}$+t-1,
令g(t)=$\frac{2t}{1+t}$-ln$\frac{2}{1+t}$-t+1,
g′(t)=ln(1+$\frac{t-1}{t+1}$)-$\frac{t-1}{t+1}$,
令$\frac{t-1}{t+1}$=x(x>0),h(x)=ln(1+x)-x,
h′(x)=$\frac{-x}{1+x}$<0,h(x)在(0,+∞)上单调递减,
∴h(x)<h(0)=0,即ln(1+x)<x,即g′(t)=ln(1+$\frac{t-1}{t+1}$)-$\frac{t-1}{t+1}$<0恒成立,
∴g(t)在(1,+∞)上是减函数,所以g(t)<g(1)=0,
∴tln$\frac{2t}{1+t}$<ln$\frac{2}{1+t}$+t-1得证,
∴$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<f′($\frac{{x}_{1}+{x}_{2}}{2}$)成立.
点评 该题考查利用导数研究函数的单调性,考查不等式的证明,考查学生的运算推理能力和转化问题的能力.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | f(b)>$\frac{1-2ln2}{4}$ | B. | f(b)<$\frac{1-2ln2}{4}$ | C. | f(b)>$\frac{3+2ln2}{8}$ | D. | f(b)<$\frac{4+3ln2}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{5π}{12}$] | C. | [$\frac{π}{12}$,$\frac{5π}{12}$] | D. | [$\frac{π}{6}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9M | B. | 9M | C. | 27M | D. | -27M |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
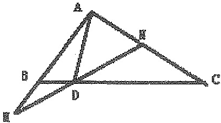 如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.
如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com