
| A�� | 10 | B�� | 9 | C�� | 8 | D�� | 11 |
���� ��$\overrightarrow{AB}��\overrightarrow{AD}$��ʾ��$\overrightarrow{AP}$���������㹲�ߵó�m��n�Ĺ�ϵ�����û�������ʽ�ó�$\frac{1}{m}$+$\frac{1}{n}$����Сֵ��
���  �⣺��$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{DC}$����$\overrightarrow{AC}=4\overrightarrow{AD}$��
�⣺��$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{DC}$����$\overrightarrow{AC}=4\overrightarrow{AD}$��
��$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AD}$��
��B��P��D���㹲�ߣ���m+4n=1��
��$\frac{1}{m}+\frac{1}{n}$=$\frac{m+4n}{m}+\frac{m+4n}{n}$=$\frac{4n}{m}+\frac{m}{n}$+5��2$\sqrt{4}$+5=9��
���ҽ���$\frac{4n}{m}=\frac{m}{n}$ʱȡ�Ⱥţ�
��ѡ��B��
���� ���⿼����ƽ�������Ļ�����������������ʽ��Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
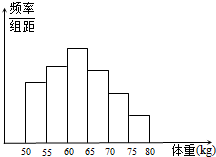 ijУ�Ը����꼶��ѧ��������죬�ֽ��������������أ���λ��kg�����ݽ���������ֳ����飬������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�һ������С���Ƶ�ʷֱ�Ϊ0.16��0.07����һ���ڶ�������С���Ƶ�ʳɵȱ����У����������ġ����塢����С���Ƶ�ʳɵȲ����У��ҵ���С���Ƶ��Ϊ236�����У�����꼶����������Ϊ��������
ijУ�Ը����꼶��ѧ��������죬�ֽ��������������أ���λ��kg�����ݽ���������ֳ����飬������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�һ������С���Ƶ�ʷֱ�Ϊ0.16��0.07����һ���ڶ�������С���Ƶ�ʳɵȱ����У����������ġ����塢����С���Ƶ�ʳɵȲ����У��ҵ���С���Ƶ��Ϊ236�����У�����꼶����������Ϊ��������| A�� | 800 | B�� | 960 | C�� | 944 | D�� | 888 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-4y+6=0 | B�� | 3x-4y-6=0 | C�� | 4x-3y+8=0 | D�� | 4x+3y-8=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��A��B��C����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�Ķ��㣬��F��c��0��Ϊ��Բ���ҽ��㣬������Ϊ$\frac{{\sqrt{3}}}{2}$������Բ����$��{2\sqrt{3}��1}��$��
��ͼ��A��B��C����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�Ķ��㣬��F��c��0��Ϊ��Բ���ҽ��㣬������Ϊ$\frac{{\sqrt{3}}}{2}$������Բ����$��{2\sqrt{3}��1}��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com