
分析 (1)由题意画出图形,数形结合得答案;
(2)设D(0,a),圆D半径为r,可得圆D的方程,把A,B的坐标用a,r表示,进一步得到PA、PB的斜率,然后利用到角公式得到tan∠APB,根据r的范围求得tan∠APB的范围.
解答 解:(1)如图,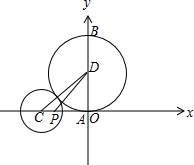
$|CD|=\sqrt{|CO{|}^{2}+|OD{|}^{2}}=5$,且圆D与圆C外切,
此时A,B的坐标分别为(0,0),(0,6),
PA在x轴上,PB斜率k=2,
∴tan∠APB=2;
(2)设D(0,a),圆D半径为r,则(r+2)2=16+a2,①
A,B坐标分别为(0,a-r),(0,a+r),
设PA、PB的斜率分别为k1,k2,则${k}_{1}=\frac{a-r}{3},{k}_{2}=\frac{a+r}{3}$,
∴$tan∠APB=\frac{\frac{a+r}{3}-\frac{a-r}{3}}{1+\frac{a+r}{3}•\frac{a-r}{3}}=\frac{6r}{{a}^{2}-{r}^{2}+9}$,②
联立①②得:tan∠APB=$\frac{6r}{4r-3}=\frac{3}{2}+\frac{9}{8r-6}$,
∵r∈[2,+∞),
∴tan∠APB∈($\frac{3}{2},\frac{12}{5}$].
点评 本题考查直线与圆的位置关系的应用,考查了到角公式的应用,考查计算能力,是中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | [0,$\frac{π}{6}$] | D. | [0,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)>$\frac{1-2ln2}{4}$ | B. | f(b)<$\frac{1-2ln2}{4}$ | C. | f(b)>$\frac{3+2ln2}{8}$ | D. | f(b)<$\frac{4+3ln2}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 8 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com