
| A. | 6 | B. | $\frac{13}{9}$ | C. | 1 | D. | $\frac{5}{9}$ |
分析 由题意可得函数的极大值或极小值等于0,求得m、n的关系,再取对数得lgn=$\frac{1}{3}$+$\frac{2}{3}$lgm,即可将问题转化为二次函数求最小值解得结论.
解答 解:∵f(x)=2mx3-3nx2+10(m,n>0)
∴f′(x)=6mx2-6nx=6x(mx-n),
∴由f′(x)=0得x=0或x=$\frac{n}{m}$,
∵f(x)=2mx3-3nx2+10(m>0)有且仅有两个不同的零点,又f(0)=10,
∴f($\frac{n}{m}$)=0,即2m•($\frac{n}{m}$)3-3n•($\frac{n}{m}$)2+10=0,整理得n3=10m2,
两边取对数得3lgn=1+2lgm,
∴lgn=$\frac{1}{3}$+$\frac{2}{3}$lgm,
∴5lg2m+9lg2n=5lg2m+9($\frac{1}{3}$+$\frac{2}{3}$lgm)2=9lg2m+4lgm+1=9(lgm+$\frac{2}{9}$)2+$\frac{5}{9}$,
∴当lgm=-$\frac{2}{9}$时,5lg2m+9lg2n有最小值为$\frac{5}{9}$.
故选D.
点评 本题考查函数的零点的判断及利用导数研究函数的极值知识,考查学生的等价转化能力及运算求解能力,属于中档题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{5π}{12}$] | C. | [$\frac{π}{12}$,$\frac{5π}{12}$] | D. | [$\frac{π}{6}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
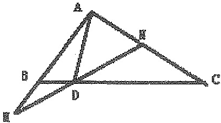 如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.
如图,在△ABC中,D是线段BC上的一点,且$\overrightarrow{BC}=4\overrightarrow{BD}$,过点D的直线分别交直线AB,AC于点M,N,若$\overrightarrow{AM}=λ\overrightarrow{AB}$,$\overrightarrow{AN}$=μ$\overrightarrow{AC}$(λ>0,μ>0),则λ+3μ的最小值是3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com