
分析 (1)根据题意,利用切线长定理,再利用双曲线的定义,把|PF1|-|PF2|=2a,转化为|HF1|-|HF2|=2a,从而求得点H的横坐标;
(2)由已知向量等式可得M为△PF1F2的内心,由三角形的面积公式作差,结合双曲线定义可得答案.
解答 (1)证明:如图所示:F1(-a,0)、F2(a,0),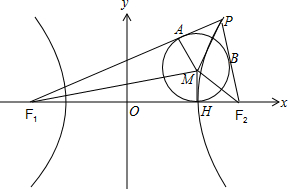
设内切圆与x轴的切点是点H,
PF1、PF2与内切圆的切点分别为A、B,
由双曲线的定义可得|PF1|-|PF2|=2a,
由圆的切线长定理知,|PA|=|PB|,故|AF1|-|BF2 |=2a,
即|HF1|-|HF2|=2a,
设内切圆的圆心横坐标为x,则点H的横坐标为x,
故 (x+c)-(c-x)=2a,
∴x=a;
(2)解:由$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{M{F}_{1}}}{|\overrightarrow{P{F}_{1}}|}$=$\frac{\overrightarrow{{{F}_{2}F}_{1}}•\overrightarrow{M{F}_{1}}}{|\overrightarrow{{F}_{2}{F}_{1}}|}$,得$\frac{|\overrightarrow{P{F}_{1}}||\overrightarrow{M{F}_{1}}|cos∠M{F}_{1}P}{|\overrightarrow{P{F}_{1}}|}$=$\frac{|\overrightarrow{{F}_{2}{F}_{1}}||\overrightarrow{M{F}_{1}}|cos∠M{F}_{1}{F}_{2}}{|\overrightarrow{{F}_{2}{F}_{1}}|}$,
∴cos∠MF1P=cos∠MF1F2,可得M在∠PF1F2的角分线上,
又M(a,2),结合(1)可知,M为△PF1F2的内心,
∴${S}_{△PM{F}_{1}}-{S}_{△PM{F}_{2}}$=$\frac{1}{2}|P{F}_{1}|×2-\frac{1}{2}|P{F}_{2}|×2=|P{F}_{1}|-|P{F}_{2}|$=2a.
点评 本题考查直线与圆锥曲线位置关系的应用,考查了双曲线的简单性质,考查数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{21}$ | B. | $\frac{2\sqrt{29}}{3}$ | C. | 2$\sqrt{21}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1,1 | B. | -1,-1 | C. | 2,-2 | D. | 2,2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com