
分析 (1)由题意可知根据矩阵的变换$(\begin{array}{l}{x′}\\{y′}\end{array})$=$(\begin{array}{l}{1}&{a}\\{b}&{0}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$=$(\begin{array}{l}{x+ay}\\{bx}\end{array})$,求得$\left\{\begin{array}{l}{x′=x+ay}\\{y′=bx}\end{array}\right.$,将x′,y′代入直线l′:x+2y+l=0.列方程求得a和b的值;
(2)由(1)求得矩阵A,写出A的特征矩阵及特征多项式,令f(λ)=0,即可解得特征值.
解答 解:(1)设直线l:x+y-1=0的点P(x,y)在变换作用下变成P′(x′,y′),
则$(\begin{array}{l}{x′}\\{y′}\end{array})$=$(\begin{array}{l}{1}&{a}\\{b}&{0}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$=$(\begin{array}{l}{x+ay}\\{bx}\end{array})$,
即$\left\{\begin{array}{l}{x′=x+ay}\\{y′=bx}\end{array}\right.$,
P′(x′,y′)在直线l′:x+2y+l=0.
所以x+ay+2bx+l=0.
即(2b+1)x+ay+1=0,
所以$\left\{\begin{array}{l}{2b+1=-1}\\{a=-1}\end{array}\right.$,解得:a=b=-1;
(2)由(1)知矩阵A=$(\begin{array}{l}{1}&{-1}\\{-1}&{0}\end{array})$,
特征矩阵为$(\begin{array}{l}{λ-1}&{1}\\{1}&{λ}\end{array})$,
特征多项式为f(λ)=$|\begin{array}{l}{λ-1}&{1}\\{1}&{λ}\end{array}|$=λ2-λ-1,
令f(λ)=0,解得:λ1=$\frac{1-\sqrt{5}}{2}$,λ2=$\frac{1+\sqrt{5}}{2}$,
矩阵A的特征值λ1=$\frac{1-\sqrt{5}}{2}$,λ2=$\frac{1+\sqrt{5}}{2}$,.
点评 本题考查矩阵的变换,考查二阶矩阵的乘法,矩阵特征值的求法,考查计算能力,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [0,+∞) | C. | (-∞,0] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
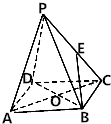 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 任务 | A | B | C | D | E | F | G |
| 所需时间/周 | 2 | 1 | 4 | 3 | 2 | 1 | 2 |
| 前期任务 | 无要求 | 无要求 | 无要求 | A,B,C | A | A,B,C,D,E | A,B,C,D,E |
| A. | 8周 | B. | 9周 | C. | 10周 | D. | 12周 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com