
分析 (I)令f′(x)=0求出f(x)的极值点,比较极值点的大小关系,利用二次函数的性质得出f(x)的单调性;
(II)讨论f(x)在(0,1)上的单调性,求出f(x)的最小值,令fmin(x)>0解出a的范围.
解答 解(Ⅰ)f′(x)=-$\frac{1}{x}$+2a(x-1)+1=$\frac{2a{x}^{2}+(1-2a)x-1}{x}$(x>0).
设g(x)=2ax2+(1-2a)x-1=(2ax+1)(x-1),
(1)当a≥0时,2ax+1>0.令g(x)>0,得x>1,令g(x)<0,得0<x<1.
∴f(x)在(1,+∞)上单调递增,在(0,1)上单调递减.
(2)当a<0时,g(x)图象开口向下,在(0,+∞)上有两个零点1和-$\frac{1}{2a}$,
①当a=-$\frac{1}{2}$时,-$\frac{1}{2a}$=1,此时当g(x)>0,无解;g(x)<0,可得x<1或x>1.
∴f(x)在(0,1),(1,+∞)上单调递减,且函数f(x)在(0,+∞)上不间断,即函数f(x)在(0,+∞)上单调递减.
②当-$\frac{1}{2}$<a<0时,-$\frac{1}{2a}>1$,此时当g(x)>0,可得1$<x<-\frac{1}{2a}$;当g(x)<0,可得0<x<1或x$>-\frac{1}{2a}$.
∴f(x)在(1,-$\frac{1}{2a}$)上单调递增;在(0,1),(-$\frac{1}{2a}$,+∞)上单调递减.
③当a<-$\frac{1}{2}$时,0$<-\frac{1}{2a}<1$,此时当g(x)>0,可得-$\frac{1}{2a}<x<1$;g(x)<0,可得0$<x<-\frac{1}{2a}$或x>1.
∴f(x)在(-$\frac{1}{2a}$,1)上单调递增;在(0,-$\frac{1}{2a}$),(1,+∞)上单调递减.
(Ⅱ)函数f(x)过(1,0)点,由(Ⅰ)得a≥-$\frac{1}{2}$时,f(x)在(0,1)为减函数,
∴f(x)>f(1)=0,符合题意.
当a<-$\frac{1}{2}$时,f(x)在(0,-$\frac{1}{2a}$)递减,在(-$\frac{1}{2a}$,1)上单调递增,
∴f(-$\frac{1}{2a}$)<f(1)=0,不符合题意.
∴a的取值范围为[-$\frac{1}{2}$,+∞).
点评 本题考查了导数与函数单调性的关系,二次不等式的解法,函数恒成立问题,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 49,9 | B. | 7,3 | C. | $\sqrt{7}$,$\sqrt{3}$ | D. | 7,$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
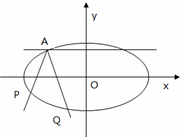 如图为焦点在x轴上的椭圆,且离心率e=$\frac{\sqrt{2}}{2}$,且过点A(-2,1),有椭圆上异于点A的点P出发的光线射到点A处被直线y=1反射后交椭圆于点Q(点Q与点P不重合).
如图为焦点在x轴上的椭圆,且离心率e=$\frac{\sqrt{2}}{2}$,且过点A(-2,1),有椭圆上异于点A的点P出发的光线射到点A处被直线y=1反射后交椭圆于点Q(点Q与点P不重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
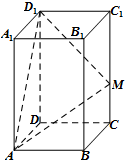 如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )
如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com