
分析 (Ⅰ)先构造函数m(x)=lnx+1-x,然后求导,根据导数符号即可求出函数m(x)的最大值为0,即得到m(x)≤0,从而证得f(x)≤x;
(Ⅱ)根据x>0,$ax+(a-1)•\frac{1}{x}-lnx-1≥0$便可解得$a≥\frac{lnx+1+\frac{1}{x}}{x+\frac{1}{x}}$,而根据上面知lnx+1≤x恒成立,从而便可求得$\frac{lnx+1+\frac{1}{x}}{x+\frac{1}{x}}$的最大值,进而即可得出实数a的取值范围.
解答 解:(Ⅰ)证明:构造函数m(x)=f(x)-x=lnx+1-x,$m'(x)=\frac{1}{x}-1=\frac{1-x}{x}=0({x>0})$得x=1;
当x∈(0,1)时,m'(x)>0;当x∈(1,+∞)时,m'(x)<0;
∴[m(x)]max=m(1)=0;
∴m(x)≤0;
∴f(x)≤x;
(Ⅱ)若g(x)≥0对x>0恒成立等价于$a≥\frac{{lnx+1+\frac{1}{x}}}{{x+\frac{1}{x}}}$对x>0恒成立;
记$G(x)=\frac{{lnx+1+\frac{1}{x}}}{{x+\frac{1}{x}}}$,问题等价于a≥G(x)max;
由(Ⅰ)知lnx+1≤x(当且仅当x=1时取得等号);
∴$G(x)=\frac{lnx+1+\frac{1}{x}}{x+\frac{1}{x}}≤\frac{x+\frac{1}{x}}{x+\frac{1}{x}}=1$(当且仅当x=1时取得等号);
故G(x)max=1,所以a≥1;
∴实数a的取值范围为[1,+∞).
点评 考查构造函数解决问题的方法,根据函数导数符号求函数最值的方法和过程,不等式的性质,在解决第二问时能用上第一问的结论很巧妙.


科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [0,+∞) | C. | (-∞,0] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
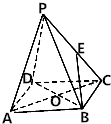 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
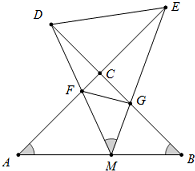 如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.
如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 现有25个字母,每个字母代表一个数字,将字母排列如表,使得表格中的各行、各列均成等差数列,若G=3,I=5,Q=9,S=19,则第一行字母代表的数字之和为-5.
现有25个字母,每个字母代表一个数字,将字母排列如表,使得表格中的各行、各列均成等差数列,若G=3,I=5,Q=9,S=19,则第一行字母代表的数字之和为-5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 任务 | A | B | C | D | E | F | G |
| 所需时间/周 | 2 | 1 | 4 | 3 | 2 | 1 | 2 |
| 前期任务 | 无要求 | 无要求 | 无要求 | A,B,C | A | A,B,C,D,E | A,B,C,D,E |
| A. | 8周 | B. | 9周 | C. | 10周 | D. | 12周 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com