
分析 (Ⅰ)利用两点间距离公式和点到直线的距离公式列出方程,由此能求出曲线C的方程,并能证明S(x,y)到点M的距离d∈[2-$\sqrt{3}$,2+$\sqrt{3}$].
(Ⅱ)设B(x0,y0),则C(-x0,-y0),代入椭圆方程,运用直线的斜率公式,化简即可得到所求值.
(Ⅲ)讨论直线PQ的斜率存在和不存在,联立直线PQ的方程和椭圆方程,求得点B的坐标,再求出直线PQ和直线PC的斜率,由此能求出结果.
解答 解:(Ⅰ)∵曲线C上的点S(x,y)到点M($\sqrt{3}$,0)的距离与它到直线x=$\frac{4}{\sqrt{3}}$的距离之比为$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{(x-\sqrt{3})^{2}+(y-0)^{2}}}{|x-\frac{4}{\sqrt{3}}|}$=$\frac{\sqrt{3}}{2}$,
整理,得$\frac{{x}^{2}}{4}+{y}^{2}$=1.
∴曲线C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
∵M($\sqrt{3},0$)是椭圆$\frac{{x}^{2}}{4}+{y}^{2}$=1的右焦点,S是椭圆上的点,
∴S(x,y)到点M的距离d∈[2-$\sqrt{3}$,2+$\sqrt{3}$].
(Ⅱ)设B(x0,y0),则C(-x0,-y0),∴$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,
∴${k}_{1}{k}_{2}=\frac{{y}_{0}}{{x}_{0}-2}•\frac{{y}_{0}}{{x}_{0}+2}$=$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-4}$=$\frac{1-\frac{1}{4}{{x}_{0}}^{2}}{{{x}_{0}}^{2}-2}$=-$\frac{1}{4}$.
(Ⅲ)联立$\left\{\begin{array}{l}{y={k}_{1}(x-2)}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,得$(1+{{k}_{1}}^{2}){x}^{2}$-4k12x+4(${{k}_{1}}^{2}-1$)=0,
解得${x}_{p}=\frac{2({{k}_{1}}^{2}-1)}{1+{{k}_{1}}^{2}}$,yP=k1(xP-2)=$\frac{-4{k}_{1}}{1+{{k}_{1}}^{2}}$,
联立$\left\{\begin{array}{l}{y={k}_{1}(x-\sqrt{2})}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k12)x2-16${{k}_{1}}^{2}$x+4(4${{k}_{1}}^{2}$-1)=0,
解得${x}_{B}=\frac{2(4{{k}_{1}}^{2}-1)}{1+4{{k}_{1}}^{2}}$,${y}_{B}={k}_{1}({x}_{B}-\sqrt{2})$=$\frac{-4{k}_{1}}{1+4{{k}_{1}}^{2}}$.
∴${k}_{BC}=\frac{{y}_{B}}{{x}_{B}}$=$\frac{-2{k}_{1}}{4{{k}_{1}}^{2}-1}$,kPQ=$\frac{{y}_{P}}{{x}_{P}+\frac{6}{5}}$=$\frac{-\frac{4{k}_{1}}{1+4{{k}_{1}}^{2}}}{\frac{2({{k}_{1}}^{2}-1)}{1+{{k}_{1}}^{2}}+\frac{6}{5}}$=$\frac{-5{k}_{1}}{4{{k}_{1}}^{2}-1}$,
∴${k}_{PQ}=\frac{5}{2}{k}_{BC}$,
∴存在常数λ=$\frac{5}{2}$,使得kPQ=$\frac{5}{2}$kBC.
点评 本题考查曲线方程的求法,考查直线的斜率乘积的求法,是中档题,解题时要认真审题,注意两点间距离公式、点到直线的距离公式、直线的斜率公式、椭圆方程的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
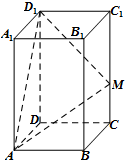 如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )
如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
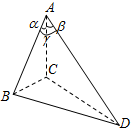 小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ.
小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com