
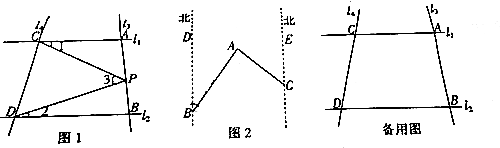
���� ��1������ƽ���ߵ����ʺ��������ڽǺͶ���������⣻
��2������ƽ���ߵ����ʺ��������ڽǺͶ���������⣻
��3����A����AF��BD����AF��BD��CE������ƽ���ߵ����ʼ�����⣻
��4���ֵ�P����A������뵱P����B���������������з������ۼ��ɣ�
���  �⣺��1����1+��2=��3��
�⣺��1����1+��2=��3��
��l1��l2��
���1+��PCD+��PDC+��2=180�㣬
�ڡ�PCD�У���3+��PCD+��PDC=180�㣬
���3=��1+��2=55�㣬
�ʴ�Ϊ��55�㣻
��2����1+��2=��3��
��l1��l2��
���1+��PCD+��PDC+��2=180�㣬
�ڡ�PCD�У���3+��PCD+��PDC=180�㣬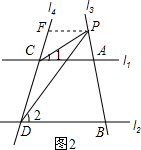
���1+��2=��3��
��3����A����AF��BD����AF��BD��CE��
���BAC=��DBA+��ACE=40��+45��=85�㣻
��4����P����A�����ʱ����ͼ2����P��PF��l1����l4��F��
���1=��FPC��
��l1��l4��
��PF��l2��
���2=��FPD
�ߡ�CPD=��FPD-��FPC
���CPD=��2-��1��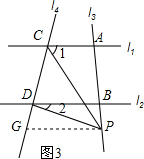
��P����B�����ʱ����ͼ3����P��PG��l2����l4��G��
���2=��GPD
��l1��l2��
��PG��l1��
���1=��CPG
�ߡ�CPD=��CPG-��GPD
���CPD=��1-��2��
���� ���⿼����ƽ���ߵ��ж������ʣ������˵���������˼�룬��������ƽ���ߵ��ж��������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
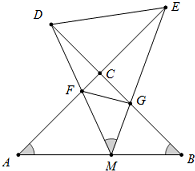 ��ͼ��MΪ�߶�AB�е㣬AE��BD���ڵ�C����DME=��A=��B=������DM��AC��F��EM��BD��G��
��ͼ��MΪ�߶�AB�е㣬AE��BD���ڵ�C����DME=��A=��B=������DM��AC��F��EM��BD��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 1��3 | C�� | 3��5 | D�� | 1��3��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com