
分析 (Ⅰ)根据极值的定义可知f'(1)=0,f(1)=$\frac{1}{6}$,进而求出a,b的值;
(Ⅱ)整理不等式得x2-x+kln(x+1)≥0在x∈[0,+∞)恒成立,构造函数g(x)=x2-x+kln(x+1),可知g(0)=0,故只需函数为增函数即可,求出导函数,对参数k进行分类讨论,得出k的范围;
(Ⅲ)令上式中k=1得x≤x2+ln(x+1)在区间[0,+∞)上恒成立,根据题型,令x=$\frac{1}{n}$,利用累加和放缩法证明结论即可.
解答 解:(Ⅰ)由题设可求得,f'(x)=3ax2+2bx,(1分)
因为f(x)在x=1处取得极值$\frac{1}{6}$,
所以f'(1)=0,f(1)=$\frac{1}{6}$(3分)
解得a=-$\frac{1}{3}$,b=$\frac{1}{2}$.(4分)
(Ⅱ)由(Ⅰ)得,f(x)=-$\frac{1}{3}$x2+$\frac{1}{2}$,所以f'(x)=-x2+x,
所以-x2+x≤kln(x+1)在x∈[0,+∞)上恒成立,
即x2-x+kln(x+1)≥0在x∈[0,+∞)恒成立.(6分)
设g(x)=x2-x+kln(x+1),则g(0)=0,
$g'(x)=2x-1+\frac{k}{x+1}=\frac{{2{x^2}+x+k-1}}{x+1}$,x∈[0,+∞).(7分)
设h(x)=2x2+x+k-1,
1)当△=1-8(k-1)≤0,即$k≥\frac{9}{8}$时,h(x)≥0,
所以g'(x)≥0,g(x)在[0,+∞)单调递增,
所以g(x)≥g(0)=0,即当$k≥\frac{9}{8}$时,满足题设条件.(8分)
2)当△=1-8(k-1)>0,即$k<\frac{9}{8}$时,
设x1,x2是方程2x2+x+k-1=0的两个实根,且x1<x2,
由$x{\;}_1+{x_2}=-\frac{1}{2}$,可知x1<0,
由题设可知,当且仅当x2≤0,即x1•x2≥0,即k-1≥0,
即k≥1时,对任意x∈[0,+∞)有h(x)≥0,
即g'(x)≥0在[0,+∞)上恒成立,
所以g(x)在[0,+∞)上为增函数,所以g(x)≥g(0)=0.
所以$1≤k<\frac{9}{8}$时,也满足题设条件.(9分)
综上可知,满足题设的k的取值范围为k≥1,所以实数k的最小值为1.(10分)
(Ⅲ)证明:由(Ⅱ)知,当k=1时,-x2+x≤ln(x+1),
即x≤x2+ln(x+1)在区间[0,+∞)上恒成立.(11分)
令$x=\frac{1}{n}(n∈{N^*})$,得$\frac{1}{n}≤\frac{1}{n^2}+ln(\frac{1}{n}+1)=\frac{1}{n^2}+ln(n+1)-lnn$.(12分)
所以当n≥2时,$\sum_{i=1}^n{\frac{1}{i}}≤1+\frac{1}{2^2}+\frac{1}{3^2}+…+\frac{1}{n^2}+(ln2-ln1)+(ln3-ln2)+…+[ln(n+1)-lnn]$
=$1+\frac{1}{2^2}+\frac{1}{3^2}+…+\frac{1}{n^2}+ln(n+1)$(13分)
$<1+\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{(n-1)n}+ln(n+1)$=$2-\frac{1}{n}+ln(n+1)<ln(n+1)+2$,
当n=1时,上式显然成立.
所以原不等式得证.(14分)
点评 考查了极值的定义,导函数判断函数的单调性,解决恒成立问题和对题型的分析,利用结论解决实际问题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
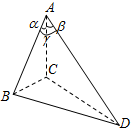 小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ.
小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com