
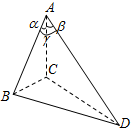
 小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ.
小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A-BCD中,已知∠BAC=α,∠CAD=β,∠DAB=γ(如图),设二面角B-AC-D的大小为θ,则cosθ=$\frac{f(λ)-cosαcosβ}{sinαsinβ}$,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=cosγ. 分析 在平面ABC内,作CB⊥AC于C,在平面ACD内作CD⊥AC于C,连接BD,则∠BCD为二面角B-AC-D的平面角,大小为θ,设AB=a,AD=b,把BC,CD,BD用含有α,β,γ及a,b的代数式表示,利用余弦定理得答案.
解答 解:如图,
在平面ABC内,作CB⊥AC于C,在平面ACD内作CD⊥AC于C,连接BD,则∠BCD为二面角B-AC-D的平面角,大小为θ,
设AB=a,AD=b,则BC=asinα,CD=bsinβ,BD2=a2+b2-2abcosγ,
∴在△BCD中,cosθ=$\frac{{a}^{2}si{n}^{2}α+{b}^{2}si{n}^{2}β-{a}^{2}-{b}^{2}+2abcosγ}{2asinα•bsinβ}$=$\frac{2abcosγ-{a}^{2}co{s}^{2}α-{b}^{2}co{s}^{2}β}{2absinαsinβ}$.
在Rt△ACB中,AC=cosα,在Rt△ACD中,AC=bcosβ,
∴a2cos2α=b2cos2β=AC2,∴a2cos2α+b2cos2β=2AC2=2abcosαcosβ,
∴$cosθ=\frac{2abcosγ-2abcosαcosβ}{2absinαsinβ}=\frac{cosγ-cosαcosβ}{sinαsinβ}$.
∴f(γ)=cosγ.
故答案为:cosγ.
点评 本题考查二面角的平面角的求法,考查三角形的解法,体现了数学转化思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
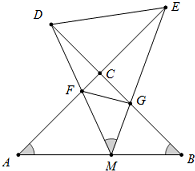 如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.
如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 任务 | A | B | C | D | E | F | G |
| 所需时间/周 | 2 | 1 | 4 | 3 | 2 | 1 | 2 |
| 前期任务 | 无要求 | 无要求 | 无要求 | A,B,C | A | A,B,C,D,E | A,B,C,D,E |
| A. | 8周 | B. | 9周 | C. | 10周 | D. | 12周 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1或3 | C. | 3或5 | D. | 1或3或5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com