练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．解方程：x2-ax-1=0．

    分析 计算判别式△=a2+4＞0，可知该二次方程由两个不等实根，由二次方程的求根公式，可得原方程的解．

    解答 解：方程x2-ax-1=0，
    由判别式△=a2+4＞0，
    可得方程有两个不等的实数根．
    由二次方程的求根公式，可得
    x1=$\frac{a+\sqrt{{a}^{2}+4}}{2}$，x2=$\frac{a-\sqrt{{a}^{2}+4}}{2}$．

    点评 本题考查含参二次方程的解法，注意运用求根公式，考查运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

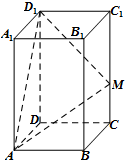    5．如图，在长方体ABCD-A1B1C1D1中，AB=1，BC=$\sqrt{3}$，点M在棱CC1上，且MD1⊥MA，则当△MAD1的面积最小时，棱CC1的长为（　　）
    A．$\frac{3}{2}$$\sqrt{2}$B．$\frac{\sqrt{10}}{2}$C．2D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

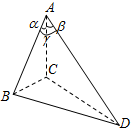    6．小明在研究三棱锥的时候，发现下面一个真命题，在三棱锥A-BCD中，已知∠BAC=α，∠CAD=β，∠DAB=γ（如图），设二面角B-AC-D的大小为θ，则cosθ=$\frac{f（λ）-cosαcosβ}{sinαsinβ}$，其中f（γ）是一个与γ有关的代数式，请写出符合条件的f（γ）=cosγ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=$\frac{2x-a}{{x}^{2}+3}$在区间[-1，1]上是增函数．
    （1）求实数a的取值范围的组成集合A．
    （2）关于x的方程f（x）=$\frac{1}{x}$的两个非零实根为x1，x2．试问是否存在实数m，使得不等式m2+tm+2≥|x1-x2|对任意a∈A及t∈[-1，1]恒成立，若存在，求m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．函数f（x）是定义在R上的奇函数，x＞0时，f（x）=2x2+2x，则x＜0时，f（x）=-2x2+2x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设f（x）是定义在正整数集上的函数，且f（x）满足：“当f（k）≥k2成立时，总可推出f（k+1）≥（k+1）2成立”．那么，下列四个命题中，正确的是②③④．（填写命题序号）
    ①若f（2）＜4成立，则f（10）＜100；②若f（3）＞9成立，则当k≥4时，均有f（k）＞k2成立；③若f（4）≥25成立，则当k≥4时，均有f（k）≥k2成立；④若f（5）＜25成立，则f（1）≤1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．若一数集的任一元素的倒数仍在该集合中，则称该数集为“可倒数集”．
    （1）判断集合A={-1，1，2}是否为可倒数集．
    （2）试写出一个含3个元素的可倒数集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．试判断下列随机试验否为古典概型，并说明理由．
    （1）在适宜条件下“种下一粒种子，观察它是否发芽”；
    （2）从市场上出售的标准为（500±5）g的袋装食盐中任取一袋，测其质量；
    （3）掷一枚骰子（骰子每个面上的点数分别为1，2，3，4，5，6），观察其朝上的点数（此骰子是由一个质地均的正方体塑料刻成的，骰子上每个的大小一样）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在平面直角坐标系xOy中，若直线l：y-$\sqrt{3}$=k（x-1）不经过第四象限，则实数k的取值范围是[0，$\sqrt{3}$]．

    查看答案和解析>>

    同步练习册答案