
分析 “当f(k)≥k2成立时,总可推出f(k+1)≥(k+1)2成立”是一种递推关系,前一个数成立,后一个数一定成立,反之不一定成立.
解答 解:①,因为“原命题成立,否命题不一定成立”,所以若f(2)<4成立,则不一定f(10)<100成立,故不正确;
②根据当f(k)≥k2成立时,总可推出f(k+1)≥(k+1)2成立,可得f(3)>9成立,则当k≥4时,均有f(k)>k2成立,正确;
③∵f(4)≥25≥16,∴对于任意的k≥4,均有f(k)≥k2成立,故正确;
④命题的逆否命题是f(x)>1,则f(5)≥25,正确,∴若f(5)<25成立,则f(1)≤1,正确.
故答案为:②③④.
点评 本题考查了命题的真假判断与应用,解题时应弄清题目中命题的含义是什么,由此能推出什么结论,是基础题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
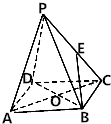 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 任务 | A | B | C | D | E | F | G |
| 所需时间/周 | 2 | 1 | 4 | 3 | 2 | 1 | 2 |
| 前期任务 | 无要求 | 无要求 | 无要求 | A,B,C | A | A,B,C,D,E | A,B,C,D,E |
| A. | 8周 | B. | 9周 | C. | 10周 | D. | 12周 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,$\frac{1}{4}$) | B. | (-∞,-$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | C. | (-$\frac{1}{4}$,0)∪(0,$\frac{1}{4}$) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 332 | B. | -332 | C. | 320 | D. | -320 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com