
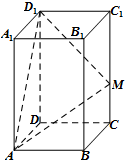
 如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )
如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=$\sqrt{3}$,点M在棱CC1上,且MD1⊥MA,则当△MAD1的面积最小时,棱CC1的长为( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 如图所示,建立空间直角坐标系.D(0,0,0),设M(0,1,t),D1(0,0,z),(z≥t≥0,z≠0).由MD1⊥MA,可得$\overrightarrow{M{D}_{1}}$•$\overrightarrow{AM}$=0,z-t=$\frac{1}{t}$.代入${S}_{△AM{D}_{1}}$=$\frac{1}{2}$|AM||MD1|,利用基本不等式的性质即可得出.
解答 解:如图所示,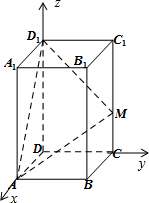 建立空间直角坐标系.
建立空间直角坐标系.
D(0,0,0),设M(0,1,t),D1(0,0,z),A($\sqrt{3}$,0,0),(z≥t≥0,z≠0).
$\overrightarrow{M{D}_{1}}$=(0,-1,z-t),$\overrightarrow{AM}$=(-$\sqrt{3}$,1,t),
∵MD1⊥MA,∴$\overrightarrow{M{D}_{1}}$•$\overrightarrow{AM}$=-1+t(z-t)=0,即z-t=$\frac{1}{t}$.
${S}_{△AM{D}_{1}}$=$\frac{1}{2}$|AM||MD1|=$\frac{1}{2}×$$\sqrt{{1}^{2}+(\sqrt{3})^{2}+{t}^{2}}$×$\sqrt{{1}^{2}+(z-t)^{2}}$
=$\frac{1}{2}$×$\sqrt{4+{t}^{2}}$$\sqrt{1+(z-t)^{2}}$=$\frac{1}{2}\sqrt{(4+{t}^{2})(1+\frac{1}{{t}^{2}})}$
=$\frac{1}{2}\sqrt{5+{t}^{2}+\frac{4}{{t}^{2}}}$≥$\frac{1}{2}\sqrt{5+2\sqrt{{t}^{2}×\frac{4}{{t}^{2}}}}$=$\frac{3}{2}$,
当且仅当t=$\sqrt{2}$,z=$\frac{3\sqrt{2}}{2}$时取等号.
故选:A.
点评 本题考查了向量垂直与数量积的关系、三角形面积计算公式、基本不等式的性质,考查了数形结合方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
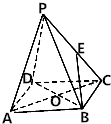 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
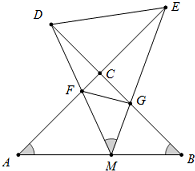 如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.
如图设M为线段AB中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com