
分析 (1)若a=1,b=1,c=1,求导数,利用导数的正负,求f(x)的单调区间;
(2)若b=c=1,且当x≥0时,f(x)≥1总成立,先确定a≥0,在分类讨论,确定函数的最小值,即可求实数a的取值范围;
(3)令f′(x)=0,x1+x2=2,x1x2=$\frac{1}{a}$,再结合基本不等式,即可证明结论.
解答 (1)解:a=1,b=1,c=1,f′(x)=$\frac{{e}^{x}({x}^{2}-x)}{({x}^{2}+x+1)^{2}}$,
∴0<x<1,f′(x)<0,x<0或x>1时,f′(x)>0,
∴函数的单调减区间是(0,1),单调增区间是(-∞,0),(1,+∞);
(2)解:若b=c=1,且当x≥0时,f(x)≥1总成立,则a≥0.
a=0,f(x)=$\frac{{e}^{x}}{x+1}$,f′(x)=$\frac{x{e}^{x}}{(x+1)^{2}}$≥0,∴f(x)min=f(0)=1;
a>0,f′(x)=$\frac{{e}^{x}•ax•(x+\frac{1-2a}{a})}{(a{x}^{2}+x+1)^{2}}$,
0<a≤$\frac{1}{2}$,f(x)min=f(0)=1;a≥$\frac{1}{2}$,f(x)在[0,$\frac{2a-1}{a}$]上为减函数,在[[$\frac{2a-1}{a}$,+∞)上为增函数,f(x)min<f(0)=1,不成立,
综上所述,0≤a≤$\frac{1}{2}$;
(3)证明:f(x)=$\frac{{e}^{x}}{a{x}^{2}+1}$,f′(x)=$\frac{{e}^{x}(a{x}^{2}-2ax+1)}{(a{x}^{2}+1)^{2}}$.
∵f(x)存在两个极值点x1,x2,∴4a2-4a>0,∴a>1.
令f′(x)=0,x1+x2=2,x1x2=$\frac{1}{a}$,f(x1)+f(x2)=$\frac{1}{2}({x}_{2}{e}^{{x}_{1}}+{x}_{1}{e}^{{x}_{2}})$>e$\sqrt{\frac{1}{a}}$,
∵$\frac{1}{2}({x}_{2}{e}^{{x}_{1}}+{x}_{1}{e}^{{x}_{2}})$<$\frac{({x}_{1}+{x}_{2})({e}^{{x}_{1}}+{e}^{{x}_{2}})}{4}$<$\frac{{e}^{2}+1}{2}$,
∴e$\sqrt{\frac{1}{a}}$<f(x1)+f(x2)<$\frac{{e}^{2}+1}{2}$.
点评 本题考查导数知识的综合运用,考查函数的单调性、最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
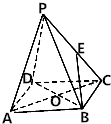 如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.
如图,正四棱锥P-ABCD的底面边长为2,侧棱长为$\sqrt{10}$,点O为底面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 现有25个字母,每个字母代表一个数字,将字母排列如表,使得表格中的各行、各列均成等差数列,若G=3,I=5,Q=9,S=19,则第一行字母代表的数字之和为-5.
现有25个字母,每个字母代表一个数字,将字母排列如表,使得表格中的各行、各列均成等差数列,若G=3,I=5,Q=9,S=19,则第一行字母代表的数字之和为-5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 任务 | A | B | C | D | E | F | G |
| 所需时间/周 | 2 | 1 | 4 | 3 | 2 | 1 | 2 |
| 前期任务 | 无要求 | 无要求 | 无要求 | A,B,C | A | A,B,C,D,E | A,B,C,D,E |
| A. | 8周 | B. | 9周 | C. | 10周 | D. | 12周 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,$\frac{1}{4}$) | B. | (-∞,-$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | C. | (-$\frac{1}{4}$,0)∪(0,$\frac{1}{4}$) | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com