
���� ��1���ɵ�T��-2��$\sqrt{3}$������Բ���ϣ���|TF1|+|TF2|=8���г����������a��b���ɴ��������Բ�ķ��̣�
��2����ֱ��OP��y=kx������$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+4{y}^{2}=16}\end{array}\right.$�����|OP|2��ͬ�����|OQ|2���ɴ���֤��|OP|2+|OQ|2Ϊ��ֵ��
��3����ֱ��l��x���ֱʱ����l��y=k��x+1������$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$���ã�1+4k2��x2+8k2x+��4k2-16��=0���Ƶ���$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{1785}{64}$����l��x�ᴹֱʱ��l��x=-1��A��-1��$\frac{\sqrt{15}}{2}$����B��-1��-$\frac{\sqrt{15}}{2}$�����Ӷ�$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{1785}{64}$���ɴ�����������
��� �⣺��1������Բ����$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��
��T��-2��$\sqrt{3}$������Բ���ϣ���|TF1|+|TF2|=8��
��$\left\{\begin{array}{l}{2a=8}\\{\frac{4}{{a}^{2}}+\frac{3}{{b}^{2}}=1}\end{array}\right.$�����a=4��b=2��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1��
֤������2����ֱ��OP��y=kx��
����������$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+4{y}^{2}=16}\end{array}\right.$����x=$��\frac{4}{\sqrt{1+4{k}^{2}}}$��
��|OP|2=${x}^{2}+{y}^{2}=\frac{16+16{k}^{2}}{1+4{k}^{2}}$��
��ֱ��OQ��$y=\frac{1}{4k}x$��
ͬ������|OQ|2=$\frac{16+16��\frac{1}{4k}��^{2}}{1+4��\frac{1}{4k}��^{2}}$=$\frac{4+64{k}^{2}}{1+4{k}^{2}}$��
��|OP|2+|OQ|2=$\frac{16+16{k}^{2}}{1+4{k}^{2}}+\frac{4+64{k}^{2}}{1+4{k}^{2}}$=$\frac{20+80{k}^{2}}{1+4{k}^{2}}$=20��Ϊ��ֵ��
�⣺��3����ֱ��l��x���ֱʱ����l��y=k��x+1����
��A��x1��y1����B��x2��y2����M��t��0����
��$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$���ã�1+4k2��x2+8k2x+��4k2-16��=0��
��$\overrightarrow{MA}$=��x1-t��y1����$\overrightarrow{MB}$=��x2-t��y2����
��$\overrightarrow{MA}•\overrightarrow{MB}$=��x1-t����x2-t��+y1y2=��x1-t����x2-t��+k��x1+1��•k��x2+1��
=��1+k2��x1x2+��k2-t����x1+x2��+��k2+t2��=$\frac{��{t}^{2}-16��+��4{t}^{2}+8t-11��{k}^{2}}{1+4{k}^{2}}$��
��$\frac{{t}^{2}-16}{1}=\frac{4{t}^{2}+8t-11}{4}$����t=-$\frac{53}{8}$����ʱ$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{1785}{64}$��
��l��x�ᴹֱʱ��l��x=-1��A��-1��$\frac{\sqrt{15}}{2}$����B��-1��-$\frac{\sqrt{15}}{2}$����
��M��-$\frac{53}{8}$��0������$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{1785}{64}$��
���ϣ�M��-$\frac{53}{8}$��0����$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\frac{1785}{64}$��
���� ���⿼����Բ���̵����������ʽΪ��ֵ��֤������������������������Ϊ��ֵ�ĵ��Ƿ���ڵ��ж��������е��⣬����ʱҪ�������⣬ע����Բ���ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
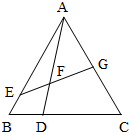 ��ͼ���ڡ�ABC�У���֪CD=2DB��BA=5BE��AF=mAD��AG=tAC��
��ͼ���ڡ�ABC�У���֪CD=2DB��BA=5BE��AF=mAD��AG=tAC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
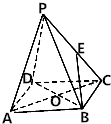 ��ͼ��������P-ABCD�ĵ���߳�Ϊ2�����ⳤΪ$\sqrt{10}$����OΪ����ABCD�����ģ�
��ͼ��������P-ABCD�ĵ���߳�Ϊ2�����ⳤΪ$\sqrt{10}$����OΪ����ABCD�����ģ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����25����ĸ��ÿ����ĸ����һ�����֣�����ĸ���������ʹ�ñ����еĸ��С����о��ɵȲ����У���G=3��I=5��Q=9��S=19�����һ����ĸ����������֮��Ϊ-5��
����25����ĸ��ÿ����ĸ����һ�����֣�����ĸ���������ʹ�ñ����еĸ��С����о��ɵȲ����У���G=3��I=5��Q=9��S=19�����һ����ĸ����������֮��Ϊ-5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\frac{1}{4}$��$\frac{1}{4}$�� | B�� | ��-�ޣ�-$\frac{1}{4}$���ȣ�$\frac{1}{4}$��+�ޣ� | C�� | ��-$\frac{1}{4}$��0���ȣ�0��$\frac{1}{4}$�� | D�� | ∅ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com