练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$；$\overrightarrow{DB}$=$\overrightarrow{a}$-$\overrightarrow{b}$．

    分析 根据平行四边形中对边平行且相等，利用向量的加法与减法运算，即可进行线性表示．

    解答 解：如图所示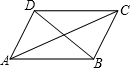，平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，
    所以$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{a}$+$\overrightarrow{b}$；
    $\overrightarrow{DB}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{a}$-$\overrightarrow{b}$．
    故答案为：$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}$-$\overrightarrow{b}$．

    点评 本题考查了平面向量的线性运算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．已知点P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右支上一点，F1、F2分别为双曲线的左、右焦点．
    （1）证明：△PF1F2的内切圆的圆心的横坐标为a；
    （2）若点M（a，2），且$\frac{\overrightarrow{P{F}_{1}}•\overrightarrow{M{F}_{1}}}{|\overrightarrow{P{F}_{1}}|}$=$\frac{\overrightarrow{{{F}_{2}F}_{1}}•\overrightarrow{M{F}_{1}}}{|\overrightarrow{{F}_{2}{F}_{1}}|}$，求△PMF1、与△PMF2的面积之差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．现有25个字母，每个字母代表一个数字，将字母排列如表，使得表格中的各行、各列均成等差数列，若G=3，I=5，Q=9，S=19，则第一行字母代表的数字之和为-5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设函数f（x）=ex+ln（x+1）-ax．
    （1）当a=2时，判断函数f（x）在定义域内的单调性；
    （2）当x≥0时，f（x）≥cosx恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．一慈善机构为筹集善款决定组织一场咅乐会．为筹备这场音乐会，必须完成A，B，C，D，E，F，G七项任务，每项任务所需时间及其关系（例如：E任务必须在A任务完成后才能进行）如表所示：
    任务ABCDEFG
    所需时间/周2143212
    前期任务无要求无要求无要求A，B，CAA，B，C，D，EA，B，C，D，E
    则完成这场音乐会的筹备工作需要的最短时间为（　　）
    A．8周B．9周C．10周D．12周

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\sqrt{x}$+$\sqrt{6-2x}$，求f（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），f′（x）为其导函数，且满足以下条件
    ①x＞0时，f′（x）＜$\frac{3f（x）}{x}$；②f（1）=$\frac{1}{2}$；③f（2x）=2f（x）
    则不等式$\frac{f（x）}{4x}$＜2x2的解集为（　　）
    A．（-$\frac{1}{4}$，$\frac{1}{4}$）B．（-∞，-$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞）C．（-$\frac{1}{4}$，0）∪（0，$\frac{1}{4}$）D．∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设a=$\int_0^π$（sinx-1+2cos2$\frac{x}{2}$）dx，则（a$\sqrt{x}$-$\frac{1}{{\sqrt{x}}}}$）6•（x2+2）的展开式中常数项是（　　）
    A．332B．-332C．320D．-320

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设集合A={x|x＜1或x＞2}，B={x|2k-1＜x≤2k+1}，且A∪B=R，则实数k的取值范围是[$\frac{1}{2}$，1）．

    查看答案和解析>>

    同步练习册答案