
分析 画出函数f(x)=$\left\{{\begin{array}{l}{\sqrt{1-{{(x-1)}^2}}}&{x∈[0,2)}\\{f(x-2)}&{x∈[2,+∞)}\end{array}}$的图象,若g(x)=0,则f(x-2)=knx,数形结合可得圆心(2n+1,0)到直线y=knx的距离为1,进而得到答案.
解答 解:当0≤x<2时,(x-1)2+y2=1,(y≥0)
其图形是以(1,0)点为圆心以1为半径的上半圆,
当x≥2时,函数f(x)=f(x-2)表示函数的周期为2,
故函数f(x)=$\left\{{\begin{array}{l}{\sqrt{1-{{(x-1)}^2}}}&{x∈[0,2)}\\{f(x-2)}&{x∈[2,+∞)}\end{array}}$的图象如下: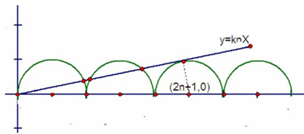
若g(x)=0,则f(x-2)=knx,
由于g(x)的零点个数为2n+1
则直线y=knx与第n+1个半圆相切,
圆心(2n+1,0)到直线y=knx的距离为1,
即$\frac{{|{{k_n}(2n+1)}|}}{{\sqrt{1+k_n^2}}}=1⇒k_n^2=\frac{1}{4}•\frac{1}{n(n+1)}=\frac{1}{4}•({\frac{1}{n}-\frac{1}{n+1}})$
有k12+k22+k32+…+kn2=$\frac{n}{4(n+1)}$.
∴$\lim_{n→+∞}$(k12+k22+k32+…+kn2)=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$
点评 本题考查的知识点是函数的图象,函数的零点,极限运算,直线与圆的位置关系,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{π}$,2] | B. | (-∞,$\frac{2}{π}$)∪[2,+∞) | C. | [0,$\frac{2}{π}$) | D. | (-∞,0)∪[$\frac{2}{π}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
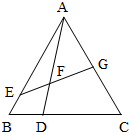 如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.
如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com