
分析 (1)通过$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+6d)}\end{array}\right.$可知公差和首项,进而可得结论;
(2)通过an=n+1,裂项可知$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,并项相加即得结论.
解答 解:(1)设数列{an}的公差为d,
∵S4=14,且a1,a3,a7成等比数列
∴$\left\{\begin{array}{l}{4{a}_{1}+6d=14}\\{({a}_{1}+2d)^{2}={a}_{1}({a}_{1}+6d)}\end{array}\right.$,
解得:d=1或d=0,
又∵等差数列{an}的各项均不相等,
∴d=1,a1=2,
∴an=a1+(n-1)d=2+(n-1)=n+1,
Sn=$\frac{n[2+(n+1)]}{2}$=$\frac{{n}^{2}+3n}{2}$;
(2)∵an=n+1,
∴$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$-$\frac{1}{n+2}$,
∴Tn=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+$…+$\frac{1}{n+1}$-$\frac{1}{n+2}$=$\frac{1}{2}$-$\frac{1}{n+2}$=$\frac{n}{2(n+2)}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
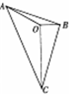 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com