
分析 (1)由二倍角公式及辅助角公式求得f(x),利用正弦函数的性质,即可求得f(x)的最大值;
(2)由(1),求得C,利用余弦定理及基本不等式的性质,即可求得△ABC面积的最大值.
解答 解:(1)由题意,$f(x)=2\sqrt{3}sinxcosx-2{cos^2}x+1$=$\sqrt{3}sin2x-cos2x=2sin(2x-\frac{π}{6})$,
当f(x)取最大值时,即$sin(2x-\frac{π}{6})=1$,此时$2x-\frac{π}{6}=2kπ+\frac{π}{2}$(k∈Z),
所以x的取值集合为$\{x|x=kπ+\frac{π}{3},k∈Z\}$.
(2)因f(C)=2,由(1)得$sin(2C-\frac{π}{6})=1$,又0<C<π,
即$-\frac{π}{6}<2C-\frac{π}{6}<\frac{11π}{6}$,所以$2C-\frac{π}{6}=\frac{π}{2}$,解得$C=\frac{π}{3}$,
在△ABC中,由余弦定理c2=a2+b2-2abcosC,
得3=a2+b2-ab≥ab,所以${S_{△ABC}}=\frac{1}{2}absinC≤\frac{{3\sqrt{3}}}{4}$,
当且仅当a=b,$C=\frac{π}{3}$,即△ABC为等边三角形时不等式取等号.
故△ABC面积的最大值为$\frac{{3\sqrt{3}}}{4}$.
点评 本题考查三角函数恒等变换,三角函数的性质,余弦定理及基本不等式的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
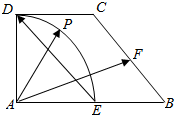 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上运动(如图所示),若 $\overrightarrow{AP}$=λ $\overrightarrow{ED}$+μ $\overrightarrow{AF}$,其中λ,μ∈R.则$\frac{2λ}{μ}$的取值范围是[-1,3].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上运动(如图所示),若 $\overrightarrow{AP}$=λ $\overrightarrow{ED}$+μ $\overrightarrow{AF}$,其中λ,μ∈R.则$\frac{2λ}{μ}$的取值范围是[-1,3].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
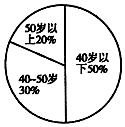 200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.
200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com