练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    执行下面的程序框图，如果输入的t∈[－1，3]，则输出的s属于(　　)

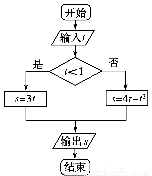
    A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5]

     

    A

    【解析】因为t∈[－1,3]，当t∈[－1,1)时，s＝3t∈[－3,3)；当t∈[1,3]时，s＝4t－t2＝－(t2－4t)＝－(t－2)2＋4∈[3,4]，所以s∈[－3，4]．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷6练习卷（解析版） 题型：解答题

    某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．

    (1)根据茎叶图计算样本均值．

    (2)日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？

    (3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷4练习卷（解析版） 题型：解答题

    如图，已知四棱锥P－ABCD的底面为直角梯形，AB∥CD，∠DAB＝90°，PA⊥底面ABCD，且PA＝AD＝DC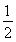＝AB＝1，M是PB的中点．

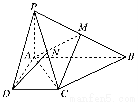
    (1)求证：AM＝CM；

    (2)若N是PC的中点，求证：DN∥平面AMC.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷3练习卷（解析版） 题型：解答题

    已知数列{2n－1·an}的前n项和Sn＝1－.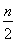

    (1)求数列{an}的通项公式；

    (2)设bn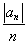＝，求数列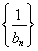的前n项和．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷3练习卷（解析版） 题型：填空题

    设数列{an}满足a1＋2a2＝3，且对任意的n∈N*，点列{Pn(n，an)}恒满足PnPn＋1＝(1,2)，则数列{an}的前n项和Sn为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷3练习卷（解析版） 题型：选择题

    在等差数列{an}中，首项a1＝120，公差d＝－4，若Sn≤an(n≥2)，则n的最小值为(　　)

    A．60 B．62 C．70 D．72

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷2练习卷（解析版） 题型：解答题

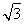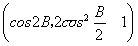    已知△ABC的内角为A、B、C，其对边分别为a、b、c，B为锐角，向量m＝(2sin B，－)，n＝，且m∥n

    (1)求角B的大小；

    (2)如果b＝2，求S△ABC的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：解答题

    已知函数f(x)＝ax2－ln x，x∈(0，e]，其中e是自然对数的底数，a∈R.

    (1)当a＝1时，求函数f(x)的单调区间与极值；

    (2)是否存在实数a，使f(x)的最小值是3？若存在，求出a的值；若不存在，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练A组练习卷（解析版） 题型：解答题

    如图，已知椭圆C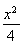：＋y2＝1，A、B是四条直线x＝±2，y＝±1所围成的两个顶点．

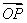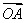    (1)设P是椭圆C上任意一点，若＝m＋n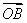，求证：动点Q(m，n)在定圆上运动，并求出定圆的方程；

    (2)若M、N是椭圆C上两上动点，且直线OM、ON的斜率之积等于直线OA、OB的斜率之积，试探求△OMN的面积是否为定值，说明理由．

     

    查看答案和解析>>

    同步练习册答案