
分析 (1)求函数定义域、导数,按照a≥0,a<0两种情况讨论f′(x)的符号变化,由极值定义可得结论;
(2)先由条件求出g(x),存在x∈(0,+∞),使得g(x)<$\frac{x-m+3}{\sqrt{x}}$成立,即m<x-$\sqrt{x}$ex+3成立.令h(x)=x-$\sqrt{x}$ex+3,x∈(0,+∞),则问题等价于m<h(x)max,利用导数基本不等式可求得h(x)max;
(3)当a=0时,令φ(x)=g(x)-f(x)-2=ex-lnx-2,利用导数表示出φ(x)的最小值,只需说明最小值大于零即可.
解答 解:(1)∵f(x)=ax+lnx,x>0,
∴f′(x)=a+$\frac{1}{x}$,
当a≥0时,f′(x)>0恒成立,
∴f(x)在(0,+∞)上单调递增,函数无极值,
当a<0时,
令f′(x)>0,解得0<x<-$\frac{1}{a}$,函数f(x)单调递增,
令f′(x)<0,解得x>-$\frac{1}{a}$,函数f(x)单调递减,
当x=-$\frac{1}{a}$时,函数有极大值,极大值为f(-$\frac{1}{a}$)=-1+ln(-$\frac{1}{a}$)=-1-ln(-a),无极小值;
(2)证明:?x∈(0,+∞),使得g(x)<$\frac{x-m+3}{\sqrt{x}}$成立.
∴?x∈(0,+∞),m<x+3-$\sqrt{x}$ex,
设h(x)=x+3-$\sqrt{x}$ex,
∴m<h(x)max,
∴h′(x)=1-ex($\frac{1}{2}{x}^{-\frac{1}{2}}$+${x}^{\frac{1}{2}}$),
∵$\frac{1}{2}{x}^{-\frac{1}{2}}$+${x}^{\frac{1}{2}}$≥2$\sqrt{\frac{1}{2}{x}^{-\frac{1}{2}}•{x}^{\frac{1}{2}}}$=$\sqrt{2}$,
∴h′(x)<0,
∴h(x)在(0,+∞)上为减函数,
∴h(x)<h(0)=3,
∴m≤3,
故m的取值范围为(-∞,3];
(3)a=0时,f(x)=lnx
令φ(x)=g(x)-f(x)-2,则φ(x)=ex-lnx-2,
∴φ′(x)=ex-$\frac{1}{x}$,且φ'(x)在(0,+∞)上为增函数,
设φ′(x)=0的根为x=t,则et=$\frac{1}{t}$,即t=e-t,
∵当x∈(0,t)时,φ'(x)<0,φ(x)在(0,t)上为减函数,
当x∈(t,+∞)时,φ'(x)>0,φ(x)在(t,+∞)上为增函数,
∴φ(x)min=φ(t)=et-lnt-2=et-lne-t-2=et+t-2.
∵φ'(1)=e-1>0,φ′($\frac{1}{2}$)=$\sqrt{e}$-2,
∴t∈($\frac{1}{2}$,1)
由于函数y=ex+x-2在上为增函数,
∴φ(x)min=φ(t)=et+t-2>e,
∴g(x)-f(x)>2.
点评 该题考查恒成立问题、利用导数研究函数的极值最值,考查基本不等式,考查分类整合思想、转化思想,考查学生综合运用知识分析解决问题的能力.注意认真体会(3)问中二次求导的应用.


科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.“ ”是“函数
”是“函数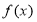 是奇函数”的充要条件
是奇函数”的充要条件
B.命题“若 ,则
,则 ”的否命题是“若
”的否命题是“若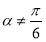 ,则
,则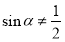 ”
”
C.若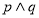 为假命题,则
为假命题,则 均为假命题
均为假命题
D.若 ,
, ,则
,则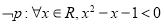
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
观察下列散点图,其中两个变量的相关关系判断正确的是( )
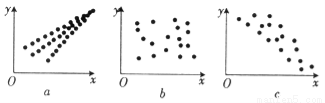
A. 为正相关,
为正相关,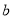 为负相关,
为负相关,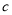 为不相关
为不相关
B.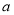 为负相关,
为负相关,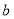 为不相关,
为不相关,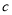 为正相关
为正相关
C.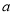 为负相关,
为负相关,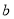 为正相关,
为正相关,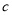 为不相关
为不相关
D.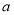 为正相关,
为正相关,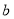 为不相关,
为不相关, 为负相关
为负相关
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
运行下面的程序,若 ,则输出的
,则输出的 等于( )
等于( )

A.9 B.7 C.13 D.11
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
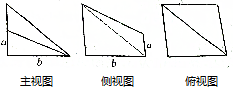
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com