
| A. | (2,+∞) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
分析 根据题意x∈[1,+∞)时,x-2k∈[1-2k,+∞);讨论①1-2k≤0时和②1-2k>0时,存在x∈[1,+∞),使f(x-2k)-k<0时k的取值范围即可.
解答 解:根据题意,x∈[1,+∞)时,x-2k∈[1-2k,+∞);
①当1-2k≤0时,解得k≥$\frac{1}{2}$;存在x∈[1,+∞),使得f(x-2k)-k<0,
即只要f(1-2k)-k<0即可;
∵1-2k≤0,∴f(1-2k)=-(1-2k)2,
∴-(1-2k)2-k<0,整理得-1+4k-4k2-k<0,即4k2-3k+1>0;
∵△=(-3)2-16=-7<0,
∴不等式对一切实数都成立,∴k≥$\frac{1}{2}$;
②当1-2k>0时,解得k<$\frac{1}{2}$;
存在x∈[1,+∞),使得f(x-2k)-k<0,
即只要f(1-2k)-k<0即可;
∵1-2k>0,∴f(1-2k)=(1-2k)2,
∴(1-2k)2-k<0,整理得4k2-5k+1<0,解得$\frac{1}{4}$<k<1;
又∵k<$\frac{1}{2}$,∴$\frac{1}{4}$<k<$\frac{1}{2}$;
综上,k∈($\frac{1}{4}$,$\frac{1}{2}$)∪[$\frac{1}{2}$,+∞)=($\frac{1}{4}$+∞);
∴k的取值范围是k∈($\frac{1}{4}$,+∞).
故选:D.
点评 本题考查了含有字母系数的不等式的解法与应用问题,也考查了分类讨论思想与转化思想的应用问题,是难题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
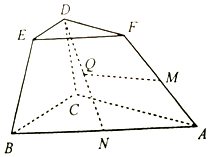 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
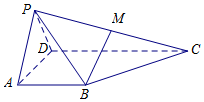 在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com