
【题目】已知函数![]() 对于任意的
对于任意的![]() 都有
都有![]() ,当
,当![]() 时,则
时,则![]() 且
且![]()
(1)判断![]() 的奇偶性;
的奇偶性;
(2)求![]() 在
在![]() 上的最大值;
上的最大值;
(3)解关于![]() 的不等式
的不等式![]() .
.
【答案】(1) 函数f(x)为奇函数.
(2)6.
(3)见解析.
【解析】
分析:(1)取x=y=0可得f(0)=0;再取y=﹣x代入即可;
(2)先判断函数的单调性,再求函数的最值;
(3)由于f(x)为奇函数,整理原式得 f(ax2)+f(﹣2x)<f(ax)+f(﹣2);即f(ax2﹣2x)<f(ax﹣2);再由函数的单调性可得ax2﹣2x>ax﹣2,从而求解.
详解:(1)取x=y=0,
则f(0+0)=f(0)+f(0);
则f(0)=0;
取y=﹣x,则f(x﹣x)=f(x)+f(﹣x),
∴f(﹣x)=﹣f(x)对任意x∈R恒成立
∴f(x)为奇函数;
(2)任取x1,x2∈(﹣∞,+∞)且x1<x2,则x2﹣x1>0;
∴f(x2)+f(﹣x1)=f(x2﹣x1)<0;
∴f(x2)<﹣f(﹣x1),
又∵f(x)为奇函数
∴f(x1)>f(x2);
∴f(x)在(﹣∞,+∞)上是减函数;
∴对任意x∈[﹣3,3],恒有f(x)≤f(﹣3)
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=﹣2×3=﹣6;
∴f(﹣3)=﹣f(3)=6;
∴f(x)在[﹣3,3]上的最大值为6;
(3)∵f(x)为奇函数,
∴整理原式得 f(ax2)+f(﹣2x)<f(ax)+f(﹣2);
即f(ax2﹣2x)<f(ax﹣2);
而f(x)在(﹣∞,+∞)上是减函数,
∴ax2﹣2x>ax﹣2;
∴(ax﹣2)(x﹣1)>0.
∴当a=0时,x∈(﹣∞,1);
当a=2时,x∈{x|x≠1且x∈R};
当a<0时,![]() ;
;
当0<a<2时,![]()
当a>2时,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.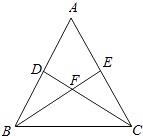
(1)求证:ADAB=AEAC;
(2)求线段BC的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系,
(万件)之间满足关系, (其中
(其中![]() 为常数,且
为常数,且![]() ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sinωx(ω>0),将f(x)的图象向左平移 ![]() 个单位从长度后,所得图象与原函数的图象重合,则ω的最小值为( )
个单位从长度后,所得图象与原函数的图象重合,则ω的最小值为( )
A.![]()
B.3
C.6
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽样调查中测得样本的6组数据,得到一个变量![]() 关于
关于![]() 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数![]() 加以说明
加以说明![]() 与
与![]() 之间存在线性相关关系(当
之间存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 关于
关于![]() 的回归方程并预测当
的回归方程并预测当![]() 时,对应的
时,对应的![]() 值为多少(
值为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() ,相关系数
,相关系数![]() 公式为:
公式为: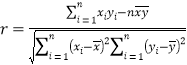 .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=2py(p>0),点A(p, ![]() )到抛物线C1的准线的距离为2.
)到抛物线C1的准线的距离为2.
(1)求抛物线C1的方程;
(2)过点A作圆C2:x2+(y﹣a)2=1的两条切线,分别交抛物线于M,N两点,若直线MN的斜率为﹣1,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励市民节约用电,实行“阶梯式”电价,某边远山区每户居民月用电量划分为三档:月用电量不超过150度,按0.6元/度收费,超过150度但不超过250度的部分每度加价0.1元,超过250度的部分每度再加价0.3元收费.
(1)求该边远山区某户居民月用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)已知该边远山区贫困户的月用电量![]() (单位:度)与该户长期居住的人口数
(单位:度)与该户长期居住的人口数![]() (单位:人)间近似地满足线性相关关系:
(单位:人)间近似地满足线性相关关系:![]() (
(![]() 的值精确到整数),其数据如表:
的值精确到整数),其数据如表:
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
现政府为减轻贫困家庭的经济负担,计划对该边远山区的贫困家庭进行一定的经济补偿,给出两种补偿方案供选择:一是根据该家庭人数,每人每户月补偿6元;二是根据用电量每人每月补偿![]() (
(![]() 为用电量)元,请根据家庭人数
为用电量)元,请根据家庭人数![]() 分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
附:回归直线![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com