
����Ŀ��ij��ҵ����һ�ֲ�Ʒ�����ݾ��飬���Ʒ��![]() ���ղ���
���ղ���![]() �������֮�������ϵ,
�������֮�������ϵ, ������
������![]() ��������
Ϊ��������![]() ����֪ÿ����1����ϸ�IJ�Ʒ��ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ��ע:��Ʒ��=��Ʒ��/�������� ��
����֪ÿ����1����ϸ�IJ�Ʒ��ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ��ע:��Ʒ��=��Ʒ��/�������� ��![]() ��ʾÿ����10����Ʒ����1����Ʒ������Ϊ�ϸ�Ʒ��.
��ʾÿ����10����Ʒ����1����Ʒ������Ϊ�ϸ�Ʒ��.
��1���Խ��������ֲ�Ʒÿ���ӯ����![]() ����Ԫ����ʾΪ�ղ���
����Ԫ����ʾΪ�ղ���![]() ��������ĺ�����
������������
��2�����ղ���Ϊ����ʱ���ɻ���������?
���𰸡���1��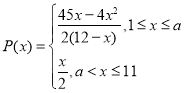 ����2��������.
����2��������.
��������
��1������ÿ���Ӯ��ΪP��x�����ղ�����x������Ʒ�ʣ�1��Q����2���ղ�����x������Ʒ�ʣ�Q����1���������ɵõ�P��x����x�ĺ���ʽ��
��2����a��x��11ʱ�����P��x�������ֵ����1��x��aʱ����12��x��t�����û�������ʽ�ɵ�x��9ʱ���Ⱥų������ʿɷ������۵ã���1��a��3ʱ����x��11ʱ��ȡ��������� 3��a��9ʱ�����ø��Ϻ����ĵ����Կɵõ�x��aʱȡ���������9��a��11ʱ�����ղ���Ϊ9���ʱ��ȡ���������
��1����![]() ʱ��
ʱ��![]() ��
��
��![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
��![]() .
.
���ϣ���ӯ����![]() ����Ԫ�����ղ���x��������ĺ�����ϵʽΪ
����Ԫ�����ղ���x��������ĺ�����ϵʽΪ
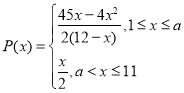 ��������a��������
��������a��������![]() ��.
��.
��2����![]() ʱ��
ʱ��![]() �������ֵΪ55��Ԫ.
�������ֵΪ55��Ԫ.
��![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ��
��
��ʱ��![]() ��
��
��Ȼ�����ҽ���![]() ����
����![]() ʱ��
ʱ��![]() �����ֵ��Ϊ13.5��Ԫ.
�����ֵ��Ϊ13.5��Ԫ.
��![]() ����
����![]() ��
��
���![]() ����ȥ����
����ȥ����![]() ��
��
��i����![]() ʱ���ղ���Ϊ11���ʱ���ɻ���������5.5��Ԫ.
ʱ���ղ���Ϊ11���ʱ���ɻ���������5.5��Ԫ.
��ii����![]() ʱ��
ʱ��![]() ʱ��
ʱ��
����![]() �ɿ������ɺ���
�ɿ������ɺ���![]() ��
��![]() ���϶��ɵ�.
���϶��ɵ�.
��Ϊ![]() ������
������![]() ����
����![]() ��
��![]() ��������
��������
��![]() ��
��![]() ��������������
��������������![]() ��
��![]() ��������
��������
�ʵ��ղ���Ϊa���ʱ���ɻ���������![]() ��Ԫ.
��Ԫ.
��iii����![]() ʱ���ղ���Ϊ9���ʱ���ɻ���������13.5��Ԫ.
ʱ���ղ���Ϊ9���ʱ���ɻ���������13.5��Ԫ.


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=xex��ax2��a��R����
��1��������g��x��= ![]() ���溯������ʵ��a��ֵ��
���溯������ʵ��a��ֵ��
��2�����������ʵ��a������h��x��=kx+b��k��bΪʵ��������ͼ���뺯��f��x����ͼ����������һ�����㣮 ����k��b��ֵ��
�ڶԣ�0��+�ޣ��ϵ�����ʵ��x1 �� x2 �� ����[f��x1����h��x1��][f��x2����h��x2��]��0����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԲC�� ![]() =1��a��b��0������ֱ��l����Բ��P��Q���㣬MΪ�߶�PQ���е㣬OΪ����ԭ�㣬��ֱ��l��б��Ϊk1 �� ֱ��OM��б��Ϊk2 �� k1k2=��
=1��a��b��0������ֱ��l����Բ��P��Q���㣬MΪ�߶�PQ���е㣬OΪ����ԭ�㣬��ֱ��l��б��Ϊk1 �� ֱ��OM��б��Ϊk2 �� k1k2=�� ![]() ��
��
��1������ԲC�������ʣ�
��2����ֱ��l��x�ύ�ڵ�D���� ![]() ��0����������
��0���������� ![]() =2
=2 ![]() ������OPQ��������ʱ������ԲC�ķ��̣�
������OPQ��������ʱ������ԲC�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �У�
�У�![]() Ϊ
Ϊ![]() �е㣬ƽ��
�е㣬ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�����Уѧ��ÿ��ʹ���ֻ�������ʱ�䣬����ռ�������λѧ��ÿ��ʹ���ֻ�������ʱ����������ݣ���λ��Сʱ�������������ݷ���Ϊ![]() ������������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪
������������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪![]() �ڵ�ѧ����5�ˣ�
�ڵ�ѧ����5�ˣ�

��1������������![]() �������Ƹ�Уѧ��ÿ��ƽ��ʹ���ֻ�������ʱ�䣻
�������Ƹ�Уѧ��ÿ��ƽ��ʹ���ֻ�������ʱ�䣻
��2����ʹ���ֻ�������ʱ����![]() �ڶ���Ϊ����ʱ�俴�ֻ�����ʹ���ֻ�������ʱ����
�ڶ���Ϊ����ʱ�俴�ֻ�����ʹ���ֻ�������ʱ����![]() �ڶ���Ϊ������ʱ�俴�ֻ�������֪����������
�ڶ���Ϊ������ʱ�俴�ֻ�������֪����������![]() λѧ�������ӣ����С�����ʱ�俴�ֻ�������
λѧ�������ӣ����С�����ʱ�俴�ֻ�������![]() λѧ�����뽫�����
λѧ�����뽫�����![]() �������������������ж��ܷ��ڷ�����ĸ��ʲ�����
�������������������ж��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��Уѧ����ʱ�俴�ֻ�������йأ�
��ǰ������Ϊ��Уѧ����ʱ�俴�ֻ�������йأ�
���� | ������ | �ϼ� | |
��ʱ�俴�ֻ� | |||
����ʱ�俴�ֻ� | 15 | ||
�ϼ� | 25 |
�ο���ʽ�����ݣ�![]() ��
��
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���������
���������![]() ����
����![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]()
��1���ж�![]() ����ż�ԣ�
����ż�ԣ�
��2����![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
��3�������![]() �IJ���ʽ
�IJ���ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��1|+|x+a|�� ![]()
��1����a=��2ʱ����ʽf��x����g��x���Ľ⼯��
��2����a����1���ҵ�x��[��a��1]ʱ������ʽf��x����g��x���н⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com