Question

【题目】如图，在△ABC中，DC⊥AB于D，BE⊥AC于E，BE交DC于点F，若BF=FC=3，DF=FE=2．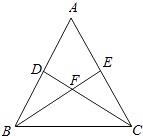

（1）求证：ADAB=AEAC；
（2）求线段BC的长度．

Answer 1

【答案】
（1）

证明：由已知∠BDC=∠BEC=90°，

所以B，C，D，E四点在以BC为直径的圆上，

由割线定理知：ADAB=AEAC

（2）

解：如图，过点F作FG⊥BC于点G，

由已知，∠BDC=90°，又因为FG⊥BC，所以B，G，F，D四点共圆，

所以由割线定理知：CGCB=CFCD，①

同理，F，G，C，E四点共圆，由割线定理知：

BFBE=BGBC，②

①+②得：CGCB+BGBC=CFCD+BFBE，

即BC2=CFCD+BFBE=3×5+3×5=30，

所以BC= ．

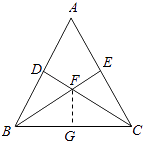
【解析】（1）推导出B，C，D，E四点在以BC为直径的圆上，由割线定理能证明ADAB=AEAC．（2）过点F作FG⊥BC于点G，推导出B，G，F，D四点共圆，F，G，C，E四点共圆，由此利用割线定理能求出BC的长．