
 ,其中x∈R,θ为参数,且0≤θ≤2π.
,其中x∈R,θ为参数,且0≤θ≤2π. 时,判断函数f(x)是否有极值;
时,判断函数f(x)是否有极值; ;(3) A的取值范围是
;(3) A的取值范围是 .
. ,解得
,解得 或
或 ,当
,当 时,可求得极小值
时,可求得极小值 ,令
,令 得
得 ,当
,当 ,所求极小值不会小于零,可得
,所求极小值不会小于零,可得 范围;(3) 函数f(x)在区间(2A-1,A)内都是增函数,则A需满足不等式组
范围;(3) 函数f(x)在区间(2A-1,A)内都是增函数,则A需满足不等式组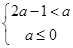 或
或 ,解得
,解得 的范围.
的范围. 时,f(x)=4x3,则f(x)在(-∞,+∞)内是增函数,故无极值. 2分
时,f(x)=4x3,则f(x)在(-∞,+∞)内是增函数,故无极值. 2分 . 3分
. 3分 时,容易判断f(x)在(-∞,0],
时,容易判断f(x)在(-∞,0], 上是增函数,在
上是增函数,在 上是减函数,
上是减函数, 处取得极小值
处取得极小值 5分
5分 ,即
,即 ,可得
,可得 .
. 或
或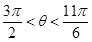 . 7分
. 7分 时,f(x)在x=0处取得极小值
时,f(x)在x=0处取得极小值 ,此时,当f(0)>0时,
,此时,当f(0)>0时, ,与
,与 相矛盾,所以当
相矛盾,所以当 时,f(x)的极小值不会大于零.
时,f(x)的极小值不会大于零. . 9分
. 9分 内都是增函数,由题设:函数在(2A-1,A)内是增函数,则A需满足不等式组
内都是增函数,由题设:函数在(2A-1,A)内是增函数,则A需满足不等式组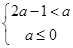 或
或 (其中θ∈
(其中θ∈ 时,
时, ). 12分
). 12分 ,
, . 14分
. 14分

科目:高中数学 来源:不详 题型:单选题
 cos2x的最小正周期和振幅分别是( )
cos2x的最小正周期和振幅分别是( )| A.π,1 | B.π,2 | C.2π,1 | D.2π,2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com