
���� ��1�������⣺������e=$\frac{{\sqrt{3}}}{2}$��AΪ�㣬��A��-a��0������A���϶������$\sqrt{5}$���ɵã�a2+b2=5��
������Բ��a��b��c�Ĺ�ϵ�������a��b��ֵ���ɵ�C���̣�
��2�������⣺P��QΪ���������㣬AΪ�㣬PQ��ԭ�㣬������Բ�ĶԳ��ԣ���֪P��Q�������ԭ��Գƣ����P�����꣬�ɵ�Q�����꣬���PA��QA�����������y�ύ��M��N�����꣬���ɵ�$\overrightarrow{AM}•\overrightarrow{AN}$��
��3�����õ�бʽ���PQֱ�߷��̣������ҳ���ʽ����᳤������ʽ��ϵ���k��ֵ��
��� �⣺��1�������⣺������e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$��AΪ�㣬��A��-a��0������A���϶������$\sqrt{5}$��
�ɵã�a2+b2=5��
����Ϊa2-b2=c2��
��ã�a=2��b=1��c=$\sqrt{3}$
����C����Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2�������⣺P��QΪ���������㣬AΪ�㣬PQ��ԭ�㣬��P��x1��y1����������Բ�ĶԳ��ԣ���֪Q
��-x1��-y1��
��${k}_{AP}=\frac{{y}_{1}}{{x}_{1}+2}$��${k}_{QA}=\frac{{y}_{1}}{-2+{x}_{1}}$
�ɵã�ֱ��PA�ķ���Ϊ��$y=\frac{{y}_{1}}{{x}_{1}+2}��x+2��$
ֱ��QA�ķ���Ϊ��$y=\frac{{-y}_{1}}{{2-x}_{1}}$��x+2��
PA��QA�ij�������y�ύ��M��N�����꣬
��x=0����ã�M��0��$\frac{2{y}_{1}}{{x}_{1}+2}$����N��0��$\frac{2{y}_{1}}{{x}_{1}-2}$����
$\overrightarrow{AM}=��2��\frac{2{y}_{1}}{{x}_{1}+2}��$��$\overrightarrow{AN}$=��2��$\frac{2{y}_{1}}{{x}_{1}-2}$����
��ô��$\overrightarrow{AM}•\overrightarrow{AN}$=4+$\frac{4{{y}_{1}}^{2}}{{{x}_{1}}^{2}-4}$��
��${{x}_{1}}^{2}+4{{y}_{1}}^{2}=4$
��$\overrightarrow{AM}•\overrightarrow{AN}$=5��������
����$\overrightarrow{AM}•\overrightarrow{AN}$�Ƕ�ֵ���䶨ֵΪ5��
��3��PQ���ҽ��㣬���ҽ���F��$\sqrt{3}$��0����
��k���ڣ�
��ֱ��PQ����Ϊy=k��x-$\sqrt{3}$������$kx-y-k\sqrt{3}=0$
����$\left\{\begin{array}{l}{{x}^{2}+4{y}^{2}=4}\\{kx-y-k\sqrt{3}=0}\end{array}\right.$������������$��4{k}^{2}+1��{x}^{2}-8\sqrt{3}{k}^{2}x+12{k}^{2}-4=0$��
${x}_{1}+{x}_{2}=\frac{8\sqrt{3}{k}^{2}}{4{k}^{2}+1}$��${x}_{1}•{x}_{2}=\frac{12{k}^{2}-4}{4{k}^{2}+1}$
���ҳ�|PQ|���ڶ��᳤��
�ɵã�|PQ|=$\sqrt{1+{k}^{2}}•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=2
���k=$��\frac{\sqrt{2}}{2}$��
���Ե�PQ���ҽ��㣬б��Ϊ$��\frac{\sqrt{2}}{2}$ʱ��|PQ|���ڶ��᳤��
���� ���⿼������Բ�ļ������ʣ�ֱ������Բ��λ�ù�ϵ�����úͼ����������ۺ���ǿ��������������ƽ�����������������㣬�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2��}{3}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{2}$ | D�� | $\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰��f��x�������ں�������f��x�������Ǻ������ķ������ǡ���f��x�������ں�������f��x���������Ǻ����� | |
| B�� | ���⡰?x0��R��ʹ�ò���ʽx2+1��0�������ķ��ǡ�?x∉R��ʹ�ò���ʽx2+1��0������ | |
| C�� | �ڡ�ABC�У���sinA��sinB���ǡ�A��B���ij�Ҫ���� | |
| D�� | ���ϽԲ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
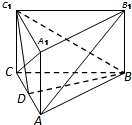 ��ͼ�����������������ⴹֱ�ڵ��棬�ҵ������������Σ�ABC-A1B1C1�У�D��AC�ߵ��е㣮
��ͼ�����������������ⴹֱ�ڵ��棬�ҵ������������Σ�ABC-A1B1C1�У�D��AC�ߵ��е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�����������ͼ��ͼ��ʾ��P��������ABCD�Խ��ߵĽ��㣬G��PB���е㣮
ij�����������ͼ��ͼ��ʾ��P��������ABCD�Խ��ߵĽ��㣬G��PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
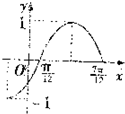 ������y=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$����ͼ������ƽ��$\frac{��}{12}$����λ���Ⱥ��������ߵ�һ������ͼ��ʾ����أ��յ�ֵ�ֱ�Ϊ��������
������y=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$����ͼ������ƽ��$\frac{��}{12}$����λ���Ⱥ��������ߵ�һ������ͼ��ʾ����أ��յ�ֵ�ֱ�Ϊ��������| A�� | 1��$\frac{��}{6}$ | B�� | 1��$-\frac{��}{6}$ | C�� | 2��$\frac{��}{3}$ | D�� | 2��$-\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com