练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某人午休醒来，发觉表停了，他打开收音机想收听电台整点报时，则他等待的时间短于5分钟的概率为（　　）
    A、
    1
    12
    B、
    1
    6
    C、
    2
    5
    D、
    1
    4
    考点：几何概型
    专题：概率与统计
    分析：由于电台的整点报时之间的间隔60分，等待的时间不多于5分钟，根据几何概率的计算公式可求．
    解答： 解：设电台的整点报时之间某刻的时间x，
    由题意可得，0≤x≤60
    等待的时间不多于5分钟的概率为P=
    5
    60
    =
    1
    12
    ；
    故选A．
    点评：本题主要考查了几何概率中与区间长度有关的概率的求解，几何概率常见的度量有区域的①长度，②面积，③体积．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图是某建筑设计院为海南国际展览馆的主展厅的屋面和水平主梁位于中轴线一侧的垂直截面的设计图，设计师以屋面曲线C和水平主梁L的交噗O为原点，水平主梁所在直线为x轴建立直角坐标系xOy，设计要求如下：屋面曲线C方程为y=
    		x
    （x≥0），水平主梁对屋面曲线的支撑构成正三角形（称为支梁三角形）：△OP1Q1，△Q1P2Q2，△Q2P3Q3，…，△Qn-1PnQn（n∈N*），其中P1，P2，P3，…Pn在屋面曲线C上，O，Q1，Q2，Q3，…，Qn在水平主梁上，记△OP1Q1的边长为a1（米），△Qk-1PkQk的边长为ak（米）（k=1，2，…，n，Q0为坐标原点O），请你解答如下问题：
    （Ⅰ）求a1，a2的值，并推导ak关于k的表达式；
    （Ⅱ）记△Qk-1PkQk的面积为bk，Tn=b1+b2+…bn，△OPnQn的面积为tn，定义δ n=
    Tn
    tn
    为防震系数，若要求防震系数为0.7，问共需要设计多少个支梁三角形？（参考公式12+22+…n2=
    n(n+1)(2n+1)
    6
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=4sinxcos（x+
    π
    3
    ）+
    		3

    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）求f（x）在区间[-
    π
    4
    ，
    π
    6
    ]    上的最大值和最小值及取得最值时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinα=
    2
    3
    ，α∈（
    π
    2
    ，π），cosβ=-
    3
    4
    ，β∈（π，
    3π
    2
    ），求sin（α-β），cos（α+β），tan（α+β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cos（
    π
    4
    +θ）=
    3
    5
    ，且
    π
    4
    +θ∈（-
    π
    2
    ，0），求
    sin2θ+2sin2θ
    1-tanθ
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    OA
    =（3，4），
    OB
    =（6，-3），
    OC
    =（5-x，-3-y）（其中O为坐标原点）．
    （1）若A，B，C三点共线，求y关于x的表达式；
    （2）若△ABC是以∠B为直角的等腰三角形，求x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

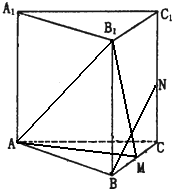    如图所示，正三棱柱ABC-A1B1C1中，各棱长均为4，M、N分别是BC、CC1的中点．
    （1）证明：MN⊥平面AMB；
    （2）求三棱锥B1-ABC的侧面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    -2x+1
    2x+1+a
    （a∈R，a＞0）．
    （1）判断函数f（x）的奇偶性，并说明理由；
    （2）当a=2时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ex-1，g（x）=-x2+4x-3，若有f（a）=g（b），则a的取值范围为（　　）
    A、[2-
    		2
    ，2+
    		2
    ]
    B、（-∞，ln2]
    C、（2-
    		2
    ，2+
    		2
    ）
    D、（ln2，+∞）

    查看答案和解析>>

    同步练习册答案