
����Ŀ��ij��ѧ������һ��������֪ʶ���������Ϊ���˽Ȿ�ξ���ѧ���ɼ���������г�ȡ�˲���ѧ���ķ������÷�ȡ������������Ϊ100�֣���Ϊ��������������Ϊn������ͳ�ƣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ķ�������Ƶ�ʷֲ�ֱ��ͼ�����������������ľ�Ҷͼ��ͼ�н��г��˵÷���
�ķ�������Ƶ�ʷֲ�ֱ��ͼ�����������������ľ�Ҷͼ��ͼ�н��г��˵÷���![]() ��
��![]() �����ݣ���
�����ݣ���
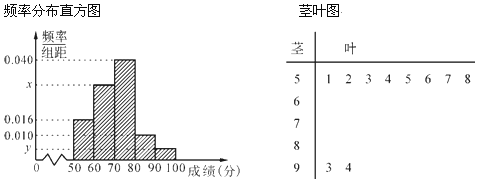
��1������������n��Ƶ�ʷֲ�ֱ��ͼ��x��y��ֵ;
��2����ѡȡ�������У��Ӿ����ɼ���80�����ϣ���80�֣���ͬѧ�������ȡ2��ͬѧ�������㳡�μӻ���֪ʶ������־Ը���������ȡ��2��ͬѧ���Բ�ͬ��ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
���������(1) ![]() ������������8����Ƶ��������������Ƶ�ʵ���
������������8����Ƶ��������������Ƶ�ʵ���![]() ������Ƶ�ʵļ��㹫ʽ�õ�
������Ƶ�ʵļ��㹫ʽ�õ�![]() ��
��![]() ��Ƶ��Ϊ2����ô�����Ƶ��
��Ƶ��Ϊ2����ô�����Ƶ��![]() ���ڸ���Ƶ�ʺ͵���1����
���ڸ���Ƶ�ʺ͵���1����![]() ��
��
��2�����ȼ���![]() ���������Լ�80�����ϵ�������������ѡ2��ͬѧ�ķ����������������һ�˵ķ���������Ȼ����������Ǹ���.
���������Լ�80�����ϵ�������������ѡ2��ͬѧ�ķ����������������һ�˵ķ���������Ȼ����������Ǹ���.
����������⣺��1���������֪����������![]()
![]()
![]() ��
��
��2���������֪��������[80��90)��5�ˣ�������[90��100)��2�ˣ��Ӿ����ɼ���80�����ϣ���80�֣���ͬѧ�������ȡ2��ͬѧ��![]() �����Σ�����21�������¼���
�����Σ�����21�������¼���
���з�������ȡ��2��ͬѧ���Բ�ͬ�����Ļ����¼���![]() ��10����
��10����
����P=10/21



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ��������Ϊ
��������Ϊ![]() , ����
, ����![]() , ����Բ����Ϊ
, ����Բ����Ϊ![]() .
.
��1������Բ�ķ��̣�
��2���费ֱ��![]() ���ֱ��
���ֱ��![]() ����Բ��
����Բ��![]() ����, ����
����, ����![]() ��������ֵ��
��������ֵ��
��3������![]() ������б�ʷֱ�Ϊ
������б�ʷֱ�Ϊ![]() ��ֱ�߽���Բ��
��ֱ�߽���Բ��![]() ���㣬��
���㣬��![]() , ��֤: ֱ��
, ��֤: ֱ��![]() ���һ������.
���һ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��ԲC��ֱ��
��ԲC��ֱ��![]() ���У�����Բ��C���ڵ�
���У�����Բ��C���ڵ�![]() �ĶԳƵ���ԲC�ϣ�ֱ��
�ĶԳƵ���ԲC�ϣ�ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��
������Բ��C�Ĺ켣E�ķ��̣�
������![]() ����ֱ��
����ֱ��![]() ����ֱ��ֱ��
����ֱ��ֱ��![]() ��Բ��C�Ĺ켣E�ཻ�ڵ�A��B����
��Բ��C�Ĺ켣E�ཻ�ڵ�A��B����![]() �����ȡֵ��Χ��
�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ�������䲼�ġ������ƽ���Сѧ����ѧ���е������,ijУ�ƻ����������ѧ���пγ̣�����ȫУѧ����ѡ��������е���(����Ҫ��ȫԱ���룬ÿ��ѧ������Ӱ��ſγ���ѡ��Ψһһ�ſγ�).���ε���������������ͼ����.
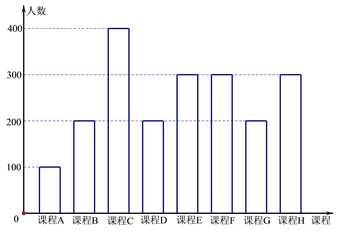
��ͼ�У���֪�γ�![]() Ϊ������γ̣��γ�
Ϊ������γ̣��γ�![]() Ϊ��Ȼ��ѧ��γ�.Ϊ��һ���о�ѧ��ѡ�����������ͼ������ȡ�ֲ����������ȫУ��ȡ
Ϊ��Ȼ��ѧ��γ�.Ϊ��һ���о�ѧ��ѡ�����������ͼ������ȡ�ֲ����������ȫУ��ȡ![]() ��ѧ����Ϊ�о�������(���¼�ơ���M��).
��ѧ����Ϊ�о�������(���¼�ơ���M��).
(��)�ڡ���M���У�ѡ��������γ̺���Ȼ��ѧ��γ̵��������ж��٣�
(��)Ϊ�μ�ij�ؾٰ����Ȼ��ѧӪ����ӡ���M������ѡ����Ȼ��ѧ��γ̵�ͬѧ�������ȡ4��ͬѧǰ��������ѡ��γ�F��γ�H��ͬѧ�μӱ��λ������Ϊÿ��1500Ԫ��ѡ��γ�G��ͬѧ�μӣ�����Ϊÿ��2000Ԫ.
(��)���������![]() ��ʾѡ����4��ͬѧ��ѡ��γ�
��ʾѡ����4��ͬѧ��ѡ��γ�![]() �����������������
�����������������![]() �ķֲ��У�
�ķֲ��У�
(��)���������![]() ��ʾѡ����4��ͬѧ�μӿ�ѧӪ�ķ����ܺͣ����������
��ʾѡ����4��ͬѧ�μӿ�ѧӪ�ķ����ܺͣ����������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn���ΪSn �� ����d��0����S3+S5=50��a1 �� a4 �� a13�ɵȱ����У�
��1��������{an}��ͨ�ʽ��
��2����{ ![]() }������Ϊ1����Ϊ2�ĵȱ����У�������{bn}ǰn���Tn ��
}������Ϊ1����Ϊ2�ĵȱ����У�������{bn}ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() x2��mlnx��g��x��=x2����m+1��x��m��0��
x2��mlnx��g��x��=x2����m+1��x��m��0��
��1������f��x���ĵ������䣻
��2����m��1ʱ�����ۺ���f��x����g��x��ͼ��Ľ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�ļ����귽��Ϊ��sin����+ ![]() ��=
��= ![]() ��
��
��1���ڼ�����ϵ��д����=0�ͦ�= ![]() ʱ��ֱ���ϵ�����ļ����꣬��������ֱ�ߣ�
ʱ��ֱ���ϵ�����ļ����꣬��������ֱ�ߣ�
��2����֪Q�����ߦ�=1�ϵ�����һ�㣬���Q��ֱ��l����̾��뼰��ʱQ�ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}�У���ai=2m��i��N* �� 3m��2��i��3m+1��m��N*����Si=ai+ai+3+ai+6+ai+9+ai+12 �� ������Si��[1000��3000]��i��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��M��AB���ӳ����ϣ�N��AD���ӳ����ϣ��ҶԽ���MN����C����֪AB=3�ף�AD=2�ף��Ǿ���AMPN�����ΪSƽ���ף� 
��1��������Ҫ����������ϵ��
��i����AN=x�ף���S��ʾΪx�ĺ�����
��ii�����BMC=�ȣ�rad������S��ʾΪ�ȵĺ�����
��2������ѡ�ã�1���е�һ��������ϵ�����S����Сֵ�������Sȡ����СֵʱAN�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com