【题目】如图，四边形ABCD是正方形，G是线段AD延长线一点，
，
平面ABCD，
，
，F是线段PG的中点；
求证：
平面PAC；
若
时，求平面PCF与平面PAG所成二面角的余弦值．
【答案】（1）见解析；（2）
【解析】
分别连接DB，DF，可得四边形BDFE为平行四边形，
又
面PAC，即可得
平面PAC；
分别以直线AB，AG，AP为x轴，y轴，z轴建立空间直角坐标系，求得平面PCF的法向量
，平面PAG的法向量为
，即可得平面PCF与平面PAG所成二面角的余弦值．
证明：分别连接DB，DF，
，F分别是线段AG，PG的中点，
，
，
又
，
，
四边形BDFE为平行四边形．
．
四边形ABCD时正方形，
，
平面ABCD，
，
，AC是面PAC内两两相交直线，
面PAC，
平面PAC；
解：分别以直线AB，AG，AP为x轴，y轴，z轴建立空间直角坐标系，
，
2，
，
2，
，
0，
，
，
．
设平面PCF的法向量，由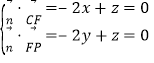
．
．
平面PAG的法向量为
．
平面PCF与平面PAG所成二面角的余弦值为．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】高考改革后，学生除了语数外三门必选外，可在A类科目：物理、化学、生物和B类科目：政治、地理、历史共6个科目中任选3门．
（1）若小明同学已经确定选了物理，现在他还要从剩余的5科中再选2科，则他在历史与地理两科中至少选一科的概率？
（2）求小明同学选A类科目数X的分布列、数学期望和方差．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的准线与双曲线
相交于
、
两点，双曲线的一条渐近线方程是
，点
是抛物线的焦点，且
是等边三角形，则该双曲线的标准方程是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图
，在边长为
的菱形
中，
，现沿对角线
把
翻折到
的位置得到四面体
，如图
所示.已知
.
（1）求证：平面
平面
；
（2）若
是线段
上的点，且
，求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将杨辉三角中的奇数换成1，偶数换成0，便可以得到如图的“0-1三角”.在“
三角”中，从第1行起，设第n
次出现全行为1时，1的个数为
，则
等于（ ）
A.13B.14C.15D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
