
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() ,下列命题:
,下列命题:
①若![]() 平行
平行![]() 内的一条直线,则
内的一条直线,则![]() ;②若
;②若![]() 垂直
垂直![]() 内的两条直线,则
内的两条直线,则![]() ;③若
;③若![]() ,
,![]() ,且
,且![]() ,
,![]() ,则
,则![]() ;④若
;④若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ;⑤若
;⑤若![]() ,
,![]() 且
且![]() ,则
,则![]() ;⑥若
;⑥若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确的命题为______(填写所有正确命题的编号).
【答案】⑤⑥
【解析】
①,根据直线与平面平行的判定定理知命题错误;
②,根据直线与平面垂直的判定定理知命题错误;
③,根据平面与平面平行的判定定理知命题错误;
④,根据平面与平面垂直的判定定理知命题错误;
⑤,由直线与平面平行的性质定理知命题正确;
⑥,由平面与平面平行的性质定理知命题正确.
对于①,若![]() 平行
平行![]() 内的一条直线,则
内的一条直线,则![]() 不一定成立,如
不一定成立,如![]() 时,
时,![]() ①错误;
①错误;
对于②,若![]() 垂直
垂直![]() 内的两条直线,则
内的两条直线,则![]() 不一定成立,如
不一定成立,如![]() 内的这两条直线平行时,
内的这两条直线平行时,![]() ②错误;
②错误;
对于③,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,则由平面与平面平行的判定定理,不能得出
时,则由平面与平面平行的判定定理,不能得出![]() ,③错误;
,③错误;
对于④,若![]() ,
,![]() ,且
,且![]() ,则由平面与平面垂直的判定定理,不能得出
,则由平面与平面垂直的判定定理,不能得出![]() ,④错误;
,④错误;
对于⑤,若![]() ,
,![]() 且
且![]() ,则由直线与平面平行的性质定理,得出
,则由直线与平面平行的性质定理,得出![]() ,⑤正确;
,⑤正确;
对于⑥,若![]() ,
,![]() ,
,![]() ,则由平面与平面平行的性质定理,即可判定
,则由平面与平面平行的性质定理,即可判定![]() ,⑥正确.
,⑥正确.
综上,其中正确的命题序号为⑤⑥.
故答案为:⑤⑥.


科目:高中数学 来源: 题型:
【题目】在下列命题中:
①方程![]() 表示的曲线所围成区域面积为
表示的曲线所围成区域面积为![]() ;
;
②与两坐标轴距离相等的点的轨迹方程为![]() ;
;
③与两定点![]() 距离之和等于
距离之和等于![]() 的点的轨迹为椭圆;
的点的轨迹为椭圆;
④与两定点![]() 距离之差的绝对值等于1的点的轨迹为双曲线.
距离之差的绝对值等于1的点的轨迹为双曲线.
正确的命题的序号是________.(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 的底面边长和侧棱长均为2,
的底面边长和侧棱长均为2,![]() 为棱
为棱![]() 的中点 .
的中点 .
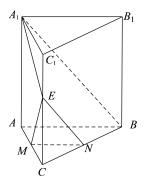
(1)证明:平面![]() 平面
平面![]() ;
;
(2)是否存在平行于![]() 的动直线
的动直线![]() ,分别与棱
,分别与棱![]() 交于点
交于点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求出点
,若存在,求出点![]() 到直线
到直线![]() 的距离;若不存在,说明理由.
的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,给定下列命题:
,给定下列命题:
①若方程![]() 有两个不同的实数根,则
有两个不同的实数根,则![]() ;
;
②若方程![]() 恰好只有一个实数根,则
恰好只有一个实数根,则![]() ;
;
③若![]() ,总有
,总有![]() 恒成立,则
恒成立,则![]() ;
;
④若函数![]() 有两个极值点,则实数
有两个极值点,则实数![]() .
.
则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级在一次理科综合检测中统计了部分“住校生”和“非住校生”共20人的物理、化学的成绩制成下列散点图(物理成绩用![]() 表示,化学成绩用
表示,化学成绩用![]() 表示)(图1)和生物成绩的茎叶图(图2).
表示)(图1)和生物成绩的茎叶图(图2).
![]()
![]()

(图1)
住校生 非住校生
2 6
9 8 5 4 4 3 1 7 4 5 7 7 9 9
6 5 8 2 2 5 7
(图2)
(1)若物理成绩高于90分,我们视为“优秀”,那么以这20人为样本,从物理成绩优秀的人中随机抽取2人,求至少有1人是住校生的概率;
(2)若化学成绩高于80分,我们视为“优秀”,根据图1完成如下列联表,并判断是否有95%的把握认为优秀率与住校有关;
住校 | 非住校 | |
优 秀 | ||
非优秀 |
附:(![]() ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)若生物成绩高于75分,我们视为“良好”,将频率视为概率,若从全年级学生中任选3人,记3人中生物成绩为“良好”的学生人数为随机变量![]() ,求出
,求出![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点M.设
相交于点M.设![]() ,
,![]() .
.

(1)试用向量![]() 表示
表示![]() .
.
(2)在线段![]() 上取点E,在线段
上取点E,在线段![]() 取点F,使
取点F,使![]() 过点M.设
过点M.设![]() ,
,![]() ,其中
,其中![]() 当
当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() ;当
;当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() .能否由此得出般结论:不论
.能否由此得出般结论:不论![]() 在线段
在线段![]() 上如何变动,等式
上如何变动,等式![]() 恒成立,请说明理由.
恒成立,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】玉山一中篮球体育测试要求学生完成“立定投篮”和“三步上篮”两项测试,“立定投篮”和“三步上篮”各有2次投篮机会,先进行“立定投篮”测试,如果合格才能参加“三步上篮”测试.为了节约时间,每项测试只需且必须投中一次即为合格.小华同学“立定投篮”的命中率为![]() ,“三步上篮”的命中率为
,“三步上篮”的命中率为![]() .假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
.假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
(1)求小华同学两项测试均合格的概率;
(2)设测试过程中小华投篮次数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com