
 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是
,据此可以预测这个孩子10岁时的身高,则正确的叙述是 | A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:单选题
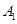 、
、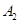 、…、
、…、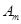 (如
(如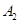 表示身高(单位:
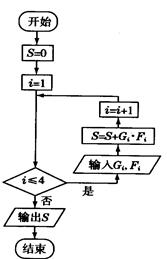
表示身高(单位: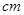 )在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180
)在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180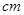 (含160
(含160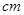 ,不含180
,不含180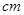 )的学生人数,那么在流程图中的判断框内应填写的条件是
)的学生人数,那么在流程图中的判断框内应填写的条件是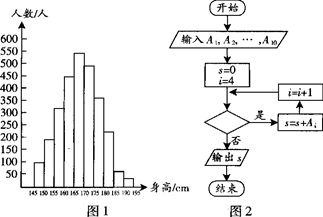
A.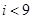 | B.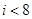 | C.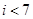 | D.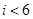 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
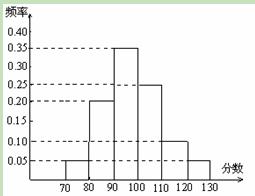
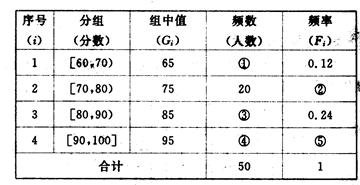
 频率分布表
频率分布表| 分组 | 频数 | 频率 | 频率/组距 |
| (10,20] | 2 | 0.10 | 0.010 |
| (20,30] | 3 | 0.15 | 0.015 |
| (30,40] | 4 | 0.20 | 0.020 |
| (40,50] | a | b | 0.025 |
| (50,60] | 4 | 0.20 | 0 .020 .020 |
(60, 70] 70] | 2 | 0.10 | 0.010 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.为60.316 kg | B.约为60.316 kg |
| C.大于60.316 kg | D.小于60.316 kg |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 课本上抄录一个随机变量
课本上抄录一个随机变量
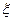 的概率分布列如下表:
的概率分布列如下表:
 同学计算
同学计算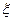 的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小王给出了正确答案
的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同.据此,小王给出了正确答案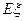 = .
= .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.粮食产量与施肥量 |
| B.高考成绩和投入复习的时间 |
| C.商品的销售额和广告费 |
| D.按定价5元销售的数的本书与销售额 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com